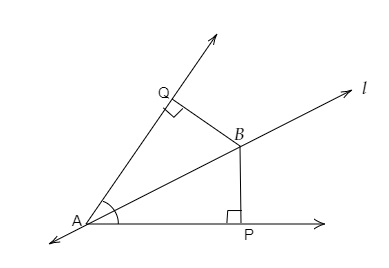
Line $ l $ is the bisector of an angle $ A $ and $ B $ is any point on $l$. BP and BQ are perpendiculars from B to the arms of $ \angle A $. Show that
(i) $ \triangle \mathrm{APB} \cong \triangle \mathrm{AQB} $
(ii) $ \mathrm{BP}=\mathrm{BQ} $ or $ \mathrm{B} $ is equidistant from the arm of angle $ \mathrm{A} $

Given:

\( l \) is the bisector of \( \angle A \) and $B$ is a point on $l$. BP and BQ are perpendiculars from $B$ to the arms of $\angle A$.

To do:

\( \angle P A B=\angle Q A B \).......(i)

\( \angle \mathrm{APB}=\angle \mathrm{AQB}=90^{\circ} \)...........(ii)

In \( \triangle \mathrm{APB} \) and \( \triangle \mathrm{AQB} \),

$\angle P A B=\angle Q A B$

$\angle \mathrm{APB}=\angle \mathrm{AQB}$

$A B=A B$       (common side)

Therefore, by AAS congruency,

$\triangle \mathrm{APB} \cong \triangle \mathrm{AQB}$

This implies,

$\mathrm{BP}=\mathrm{BQ}$            (CPCT)

Hence proved.

Tutorialspoint

Updated on: 10-Oct-2022

44 Views

Kickstart Your Career

Get certified by completing the course

Get Started