One to One Function

Introduction

One to one functions that maps every element of the range to one element of its domain. Functions are defined as relationships between a set of inputs, each with an output. Simply put, a function is a relationship between inputs, where each input is associated with one output. Each function has a domain and a codomain or range. Functions are commonly represented by 𝑓 (𝑥), where x is the input.

The general representation of a function is

$$\mathrm{y\:=\:f(x)}$$

In a mathematical sense, these relationships can be described as one-to-one functions. In this case, the number of elements is the same, or one element can only be paired with another one.

In this tutorial, we will discuss the one-to-one functions.

Functions

Functions are a special kind of relationship. Mathematical functions are usually visualized as rules that give a unique output for each input x. Mappings or transformations are used to indicate mathematical functions. These functions are usually represented by letters such as f, g, and h. A domain is defined as a set of all values that you can enter, while a function can be defined. The range contains all the values returned as the output of the function in question. The codomain is a set of values that can be output as the output of a function.

Each function has a domain and a codomain or range. Functions are commonly represented by 𝑓 (𝑥), where x is the input.

The general representation of a function is

$$\mathrm{y\:=\:f(x)}$$

Types of Functions

The different types of functions based on set elements are −

• One to One Functions

• Many One Functions

• Onto Function

• One to One and Onto Function

• Into Function

• Constant Function

One to One Function

The term one-to-one relationship actually refers to a relationship between any two objects, one of which can belong only with one other object. In a mathematical sense, these relationships can be described as one-to-one functions. In this case, the number of elements is the same, or one element can only be paired with another one.

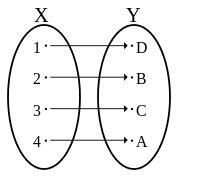
Many One Function

A many-to-one function is defined by the function $\mathrm{f\:\colon\:A\rightarrow\:B}$ so that multiple elements of set A are connected to the same element of set B. With the many-to-one feature, multiple elements share the same codomain or image. If a codomain many-to-one function has a single value.

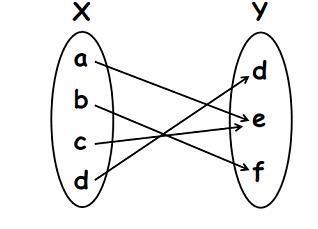
Onto Function

In the onto-function, each codomain element is associated with the domain element. For functions defined in A → B, all elements in set B have a preimage of set A. The onto function is also called surjective function.

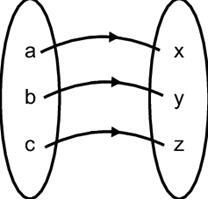
One one and Onto Function

Functions that are both one- one functions and onto functions are called bijective functions. Here, each element of the domain is mapped to a specific element within the codomain, and each element of the codomain has a prototype (pre-image). That is, all the elements in set A are associated with a particular element in set B, leaving no elements in set B.

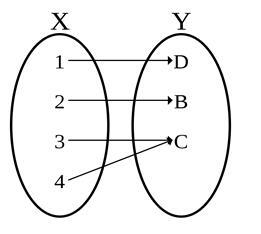
Into Functions

In terms of its properties, the Into function is the exact opposite of the Onto function. Here, there is a specific element at the end that has no pre-image (Prototype). The elements of set B are redundant and are not associated with any of the elements of set A.

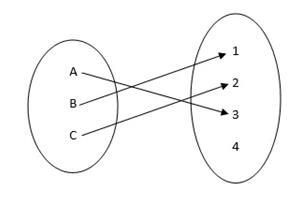
Constant Functions

These functions are an important form of many-to-one functions. In the constant function, each domain element has one image.

The format of the constant function is f (x) = K where K is a real number. Gets the K value in the same range for a constant function for different values in the range of values (x value).

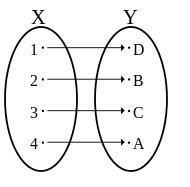
One to One (Injective) Functions

A one-to-one (Injective) function is a special type of function that maps each element of a range to exactly one element in its domain that is the outputs will not be repeated. A one-to-one function is defined by f: X → Y so that each element of set X is associated with a particular element of set Y. One-to-one functions are also known as injective functions. Here, each element of the domain has an image or codomain element that is specific to a particular function. The term one-to-one relationship actually refers to a relationship between any two objects, one of which can belong only with one other object. In a mathematical sense, these relationships can be described as one-to-one functions. In this case, the number of elements is the same, or one element can only be paired with another one.

How to prove a function is One to One

1. The best way of proving a function to be one to one or onto is by using the definitions.

A function 𝑓: 𝐴 → 𝐵 is said to be one to one (injective) if for every 𝑥, 𝑦 ∈ 𝐴, $\mathrm{f(x)\:=\:f(y)\:then\:x\:=\:y}$

This simply means that a unique element of A is mapped to a unique element of B. Let us see the function 𝑓: 𝑅 → 𝑅 defined as $\mathrm{f(x)\:=\:2x\:+\:4}$.

Now we need to prove that it is a one to one function.

Assume $\mathrm{f(x)\:=\:f(y)}$

which implies $\mathrm{2x\:+\:4\:=\:2y\:+\:4}$

or, $\mathrm{x\:=\:y}$

Hence, by definition, f(x) is one to one function.

2. Horizontal line test.

The injective function can be determined by a horizon test or a geometric test. If the horizontal line intersects the function's graph only once, the function is mapped one-to-one.

If the horizontal line intersects the function graph multiple times, the function does not match one-to-one.

Solved Examples

1) Prove that the function $\mathrm{f\colon\:R\rightarrow\:R}$ defined as $\mathrm{f(x)\:=\:6x\:+\:9}$. is a injective function or one one function.

Answer: Given that function $\mathrm{f\colon\:R\rightarrow\:R} defined as $\mathrm{f(x)\:=\:6x\:+\:9}$

Now we need to prove that it is one to one function.

Assume $\mathrm{f(x)\:=\:f(y)}$

which implies $\mathrm{6x\:+\:9\:=\:6y\:+\:9}$

or, $\mathrm{x\:=\:y}$

Hence, by definition, f(x) is one- one function.

2) Which of the following function is one one if 𝑨 = {𝟒, 𝟓, 𝟔} and 𝒂𝒏𝒅 𝑩 = {𝒑, 𝒒, 𝒓, 𝒔}.

$\mathrm{\lbrace\:(4\:,\:r)\:,\:(5\:,\:r)\:,\:(5\:,\:r)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(5\:,\:r)\:,\:(6\:,\:s)\rbrace\:}$

$\mathrm{\lbrace\:(4\:,\:p)\:,\:(4\:,\:r)\rbrace\:}$

Answer − {(4, p),(5, r),(6, s)} this is a one one function This is because the elements of set B are uniquely mapped to the elements of set A.

3) Show that the function $\mathrm{f\colon\:R\rightarrow\:R}$ 𝒅𝒆𝒇𝒊𝒏𝒆𝒅 𝒂𝒔 $\mathrm{f(x)\:=\:x^{2}\:-\:2}$ is not a one- one function.

Answer − For one one function $\mathrm{f(x)\:=\:f(y)}$

$$\mathrm{x^{2}\:-\:2\:=\:y^{2}\:-\:2}$$

$$\mathrm{\Longrightarrow\:x^{2}\:=\:y^{2}}$$

$$\mathrm{\:\:\:\:\:\:\:\:\Longrightarrow\:x^{2}\:-\:y^{2}\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:(x\:-\:y)\:(x\:+\:y)\:=\:0}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Longrightarrow\:x\:=\:y\:and\:x\:=\:-y}$$

Since we have got two relations in x and y 𝑥 = 𝑦 𝑎𝑛𝑑 𝑥 = −𝑦 hence it does not satisfy the conditions of one-one function.

Conclusion

The term one-to-one relationship actually refers to a relationship between any two objects, one of which can belong only with one other object. In a mathematical sense, these relationships can be described as one-to-one functions. In this case, the number of elements is the same, or one element can only be paired with another one.

FAQs

1. What do you mean by functions?

Functions are a special kind of relationship. Mathematical functions are usually visualized as rules that give a unique output for each input x.

2. What do you mean by one to one function?

The term one-to-one relationship actually refers to a relationship between any two objects, one of which can belong only with one other object.

3. What do you mean by onto function?

In the onto-function, each codomain element is associated with the domain element. For functions defined in A → B, all elements in set B have a preimage of set A. The onto function is also called surjective function.

4. What do you mean by one to one and onto function?

Functions that are both one-one functions and onto functions are called bijective functions. Here, each element of the domain is mapped to a specific element within the codomain, and each element of the codomain has a prototype (pre-image).

5. What do you mean by many one function?

A many-to-one function is defined by the function $\mathrm{f\colon\:A\rightarrow\:B}$ so that multiple elements of set A are connected to the same element of set B. With the many-to-one feature, multiple elements share the same codomain or image.