Monotonic Shortest Path from Source to Destination in Directed Weighted Graph

Pathfinding algorithms are based on graph search techniques that study paths between nodes, starting with one node and progressing via connections until the objective is attained. In this post, we'll talk about weighted graphs and how to calculate the monotonic shortest route between source and end node in a directed weighted graph.

What Are Weighted Graphs?

A weighted graph combines a graph with a weight function. That is, it assigns an integer weight to every edge.

There are multiple uses for edge weights for a graph −

• Network Connection Latency 

• Road Network Distances

• The Strength of a social network interaction

There are two main computational methods for representing weights −

• In adjacency lists, register edge weight for every vertex.

• Keep a distinct Set data structure that maps every edge to its weight.

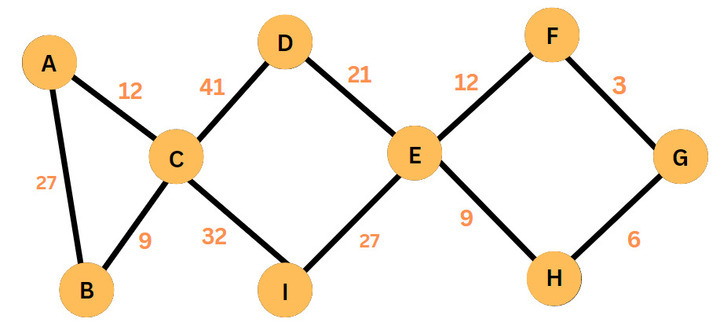
Monotonic Shortest Paths

A path is monotonic if the weight of each edge on the path is either strictly growing or strictly decreasing.

What are the Properties of Shortest Paths?

The properties of shortest paths are as follows −

• Weights are not always distances. Geometric intuition is helpful, but edge weights indicate time or cost.

• The shortest roads are always the simplest. 

• Negative weights complicate things. For now, we'll assume that the edge weights are positive (or zero).

• Paths are defined. The shortest path must maintain the direction of an edge.

• Not all vertices must be accessible. If a node is inaccessible from another, no path exists. Hence no shortest one from s to t.

• There may be numerous pathways with the lowest weight between a single vertex or node and others.

• It is possible to have parallel edges and self-loops.

Dijkstra's Shortest Path Algorithm

This method first determines the lowest-weight relationship between the start node and all immediately linked nodes. It tracks each of the weights and goes to the node that is "closest." It then repeats the calculation, but this time as a collective sum from the original node. This procedure remains this way, assessing all the incremental weights and at all times taking the least weighted collective path to the target node.

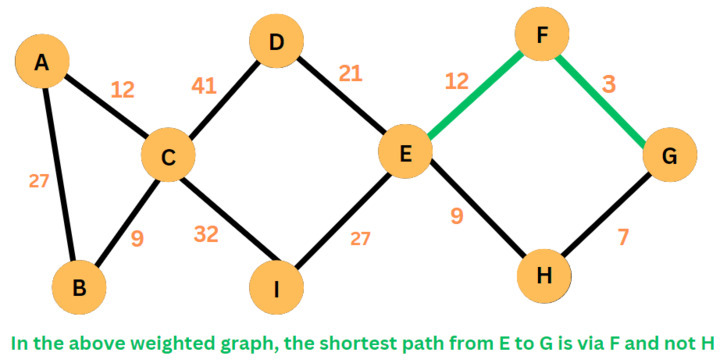
All Pairs Shortest Path (APSP) Algorithm

This finds the minimum distance path linking any two nodes. It stands faster than implementing the SSSP method for every two vertices of the network.

APSP improves processes by maintaining a count of the weights determined, thus executing several vertices simultaneously. These identified weights are utilised to find the shortest path to an unknown vertex.

When Can I Use The All Pairs Shortest Path?

When the shortest route is obstructed or suboptimal, "All Pairs Shortest Path" is typically employed to explore alternate directions. For example, this method ensures the optimal numerous pathways for diversity routing in logical route planning. When evaluating all alternative paths between all or most of your nodes, use APSP.

Single Source Shortest Path (SSSP)

The "SSSP algorithm" finds a "shortest weighted pathway" between a primary node and every node in a network.

How Does It Work?

It works in this order −

It all commences at the root node from which every pathway are assessed.

The link from the root node with the minimum weight is chosen and incorporated into the tree, combined with its associated node.

The next relationship from the root node to every unvisited node that has the minimum cumulative weight is chosen and placed into the tree in a similar manner.

As soon as there aren't any more nodes to place, the procedure is complete, and the SSSP is obtained.

When Can One Apply This Algorithm?

When one needs to determine the best path from an identified initial location to all of the other nodes, SSSP algorithm is used. Since the route is determined by the overall path weight beginning at the root, it is beneficial for determining the optimum path to every node, but it is not always necessary when all nodes must be reached in one visit.

Monotonic Shortest Path from Source to Destination In Directed Weighted Graph

Follow the instructions below to address the issue −

Run Dijkstra's algorithm twice for both increasing and decreasing pathways.

• Using "Dijkstra's for decreasing shortest routes" updates the shortest pathway from one node to another if the edge weight between the nodes is less than the edge weight of the least distanced pathway going towards the source node. 

• The same holds for growing shortest paths − Only update the shortest route from one node to another if the edge is longer than the edge of the least distanced route going towards the source.

There is no legitimate shortest path if the target vertex hasn't yet been reached.

If both Dijkstra's passes on increasing as well as decreasing shortest routes provide no viable pathways, return -1.

Example

#include <bits/stdc++.h>
#include <limits>
#include <queue>
#include <vector>
 
using namespace std;

// Represents a vertex in the graph
class Vertex {
   public:
      int id;
      vector<int> adj_list;
      vector<double> adj_weights;
 
   // A constructor which accepts the id of the vertex
   Vertex(int num)
   : id(num){
   }
};
 
// Finds the monotonic shortest path using Dijkstra's algorithm
double shortest_path(vector<Vertex>& vertices, int src, int destination){
   int N = vertices.size() - 1;
 
   // Stores distance from src and edge on the shortest path from src
   vector<double> distTo(N + 1, numeric_limits<double>::max());
   vector<double> edgeTo(N + 1, numeric_limits<double>::max());
 
   // Setting initial distance from src to the highest value
   for (int i = 1; i <= N; i++) {
      distTo[i] = numeric_limits<double>::max();
   }
 
   // Monotonic decreasing pass of Dijkstra's
   distTo[src] = 0.0;
   edgeTo[src] = numeric_limits<double>::max();
 
   priority_queue<pair<double, int>,
   vector<pair<double, int> >,
   greater<pair<double, int> > >
   pq;
   pq.push(make_pair(0.0, src));
 
   while (!pq.empty()) {
      // Take the vertex with the closest current distance from src
      pair<double, int> top = pq.top();
      pq.pop();
      int closest = top.second;
 
      for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
         int neighbor = vertices[closest].adj_list[i];
         double weight = vertices[closest].adj_weights[i];
 
         // Checks if the edges are decreasing and whether the current directed edge will create a shorter path
         if (weight < edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
            edgeTo[neighbor] = weight;
            distTo[neighbor] = distTo[closest] + weight;
            pq.push(make_pair(distTo[neighbor], neighbor));
         }
      }
   }
 
   // Store the result of the first pass of Dijkstra's
   double first_pass = distTo[destination];
 
   // Monotonic increasing pass of Dijkstra's
   for (int i = 1; i <= N; i++) {
      distTo[i] = numeric_limits<double>::max();
   }
 
   distTo[src] = 0.0;
   edgeTo[src] = 0.0;
 
   pq.push(make_pair(0.0, src));
 
   while (!pq.empty()) {
      // Take the vertex with the closest current distance from src
      pair<double, int> top = pq.top();
      pq.pop();
      int closest = top.second;
 
      for (int i = 0; i < vertices[closest].adj_list.size(); i++) {
         int neighbor = vertices[closest].adj_list[i];
         double weight = vertices[closest].adj_weights[i];
 
         // Checks if the edges are increasing and whether the current directed edge will create a shorter path
         if (weight > edgeTo[closest] && distTo[closest] + weight < distTo[neighbor]) {
            edgeTo[neighbor] = weight;
            distTo[neighbor] = distTo[closest] + weight;
            pq.push(make_pair(distTo[neighbor], neighbor));
         }
      }
   }
 
   // Store the result of the second pass of Dijkstras
   double second_pass = distTo[destination];
 
   if (first_pass == DBL_MAX && second_pass == DBL_MAX)
      return -1;
 
   return min(first_pass, second_pass);
}
 
// Driver Code
int main(){
   int N = 6, M = 9, src, target;
 
   // Create N vertices, numbered 1 to N
   vector<Vertex> vertices(N + 1, Vertex(0));
 
   for (int i = 1; i <= N; i++) {
      vertices[i] = Vertex(i);
   }
 
   // Add M edges to the graph
   vertices[1].adj_list.push_back(3);
   vertices[1].adj_weights.push_back(1.1);
 
   vertices[1].adj_list.push_back(5);
   vertices[1].adj_weights.push_back(2.0);
 
   vertices[1].adj_list.push_back(6);
   vertices[1].adj_weights.push_back(3.3);
 
   vertices[2].adj_list.push_back(5);
   vertices[2].adj_weights.push_back(2.7);
 
   vertices[3].adj_list.push_back(4);
   vertices[3].adj_weights.push_back(2.0);
 
   vertices[3].adj_list.push_back(5);
   vertices[3].adj_weights.push_back(1.1);
 
   vertices[4].adj_list.push_back(2);
   vertices[4].adj_weights.push_back(2.3);
 
   vertices[5].adj_list.push_back(6);
   vertices[5].adj_weights.push_back(2.4);
 
   vertices[6].adj_list.push_back(2);
   vertices[6].adj_weights.push_back(3.0);
 
   // src and destination vertices
   src = 1;
   target = 2;
   double shortest = shortest_path(vertices, src, target);
   cout << shortest << endl;
   return 0;
}

Output

According to the above code −

5.4

Alternative Method For Finding The Shortest Path In A Weighted Graph

The "Bellman-Ford algorithm" represents a "single-source shortest path" technique. This implies that provided a weighted network, this method will provide the minimum distance path across any two vertices.

The Bellman-Ford algorithm, compared to the Dijkstra Algorithm, may operate on graphs having edges of negative weights. Because of this, the Bellman-Ford algorithm is preferred by many.

Examples of dynamic programming include this algorithm. It starts with a single node then evaluates the distances between further vertices that may be visited using one edge. Then it proceeds to search for paths that include two edges, and the process continues. The Bellman-Ford algorithm employs a bottom-up strategy.

Conclusion

Pathfinding algorithms can assist us in understanding the links between our data. Running Dijkstra's Algorithm twice finds the least distanced path between the source and destination nodes. This method uses edge weights to find a path that reduces the collective weight across the source and all other nodes.