Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Dijkstra’s algorithm to compute the shortest path through a graph
Definition
The Dijkstra’s algorithm finds the shortest path from a particular node, called the source node to every other node in a connected graph. It produces a shortest path tree with the source node as the root. It is profoundly used in computer networks to generate optimal routes with the aim of minimizing routing costs.
Dijkstra’s Algorithm
Input − A graph representing the network; and a source node, s
Output − A shortest path tree, spt[], with s as the root node.
Initializations −
An array of distances dist[] of size |V| (number of nodes), where dist[s] = 0 and dist[u] = ∞ (infinite), where u represents a node in the graph except s.
An array, Q, containing all nodes in the graph. When the algorithm runs into completion, Q will become empty.
An empty set, S, to which the visited nodes will be added. When the algorithm runs into completion, S will contain all the nodes in the graph.
Repeat while Q is not empty −
Remove from Q, the node, u having the smallest dist[u] and which is not in S. In the first run, dist[s] is removed.
Add u to S, marking u as visited.
For each node v which is adjacent to u, update dist[v] as −
If (dist[u] + weight of edge u-v) < dist[v], Then
Update dist[v] = dist[u] + weight of edge u-v
The array dist[] contains the shortest path from s to every other node.
Example
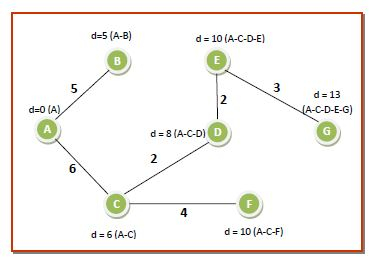
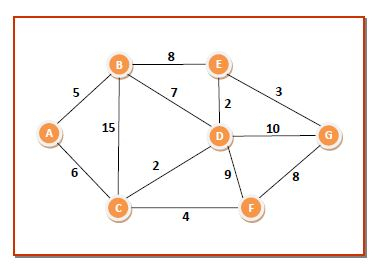
The working of the algorithm can be best understood using an example. Consider the following graph having nodes marked from A to G, connected by weighted edges as follows −
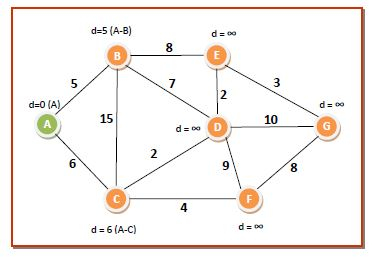
The initializations will be as follows −
dist[7]={0,∞,∞,∞,∞,∞,∞}
Q={A,B,C,D,E,F,G}
S𝑆= ∅
Pass 1 − We choose node A from Q since it has the lowest dist[] value of 0 and put it in S. The neighbouring nodes of A are B and C. We update dist[] values corresponding to B and C according to the algorithm. So the values of the data structures become −
dist[7]={0,5,6,∞,∞,∞,∞}
Q={B,C,D,E,F,G}
S={A}
The distances and shortest paths after this pass are shown in the following graph. The green node denotes the node already added to S −
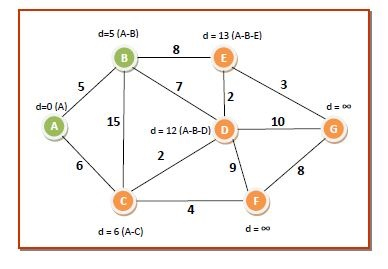
Pass 2 − We choose node B from Q since it has the lowest dist[] value of 5 and put it in S. The neighbouring nodes of B are C, D and E. We update dist[] values corresponding to C, D and E according to the algorithm. So the values of the data structures become −
dist[7]={0,5,6,12,13,∞,∞}
Q={C,D,E,F,G}
S={A,B}
The distances and shortest paths after this pass are −
Pass 3 − We choose node C from Q since it has the lowest dist[] value of 6 and put it in S. The neighbouring nodes of C are D and F. We update dist[] values corresponding to D and F. So the values of the data structures become −
dist[7]={0,5,6,8,13,10,∞}
Q={D,E,F,G}
S={A,B,C}
The distances and shortest paths after this pass are −
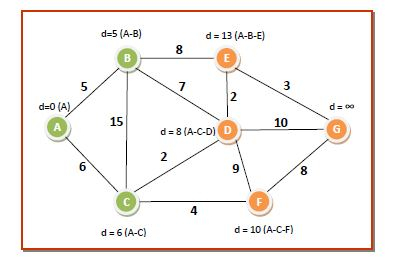
Pass 4 − We choose node D from Q since it has the lowest dist[] value of 8 and put it in S. The neighbouring nodes of D are E, F and G. We update dist[] values corresponding to E, F and G. So the values of the data structures become −
dist[7]={0,5,6,8,10,10,18}
Q={E,F,G}
S={A,B,C,D}
The distances and shortest paths after this pass are −
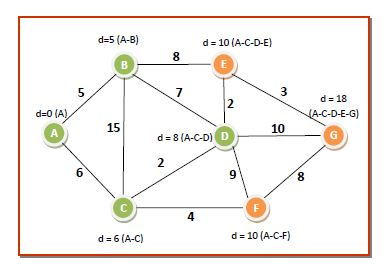
Pass 5 − We can choose either node E or node F from Q since both of them have the lowest dist[] value of 10. We select any one of them, say E, and put it in S. The neighbouring nodes of D is G. We update dist[] values corresponding to G. So the values of the data structures become −
dist[7]={0,5,6,8,10,10,13}
Q={F,G}
S={A,B,C,D,E}
The distances and shortest paths after this pass are −
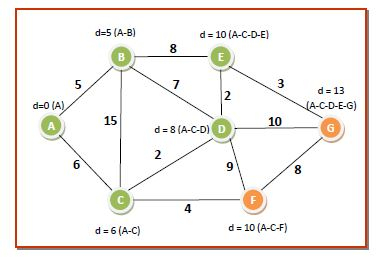
Pass 6 − We choose node F from Q since it has the lowest dist[] value of 10 and put it in S. The neighbouring nodes of F is G. The dist[] value corresponding to G is less than that through F. So it remains same. The values of the data structures become −
dist[7]={0,5,6,8,10,10,13}
Q={G}
S={A,B,C,D,E,F}
The distances and shortest paths after this pass are −
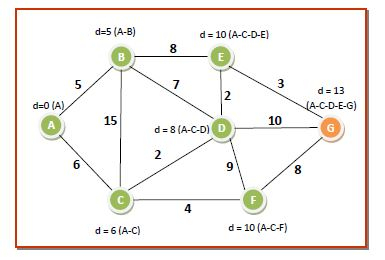
Pass 7 − There is just one node in Q. We remove it from Q put it in S. The dist[] array needs no change. Now, Q becomes empty, S contains all the nodes and so we come to the end of the algorithm. We eliminate all the edges or routes that are not in the path of any route. So the shortest path tree from source node A to all other nodes are as follows −
18K+ Views
