
- Home
- Writing a mixed number and an improper fraction for a shaded region
- Writing an improper fraction as a mixed number
- Writing a mixed number as an improper fraction
- Mixed number multiplication
- Multiplication of a mixed number and a whole number
- Division with a mixed number and a whole number
- Mixed number division
- Word problem involving multiplication or division with mixed numbers
Writing a mixed number and an improper fraction for a shaded region
In this lesson, we consider figures like circles, rectangular strips etc., some of which are shaded whole and some shaded fractionally. For combinations of whole and fractionally shaded regions, we write the corresponding mixed numbers and improper fractions that would represent them.
For example, if two whole shaded figures and a three-fifth fractionally shaded figure are given, we represent such a combination with mixed number $2\frac{4}{5}$ and improper fraction $\frac{14}{5}$.
Example 1
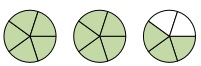
Write a mixed number for the shaded region given below
Solution
Step 1:
There are two shaded whole circles and a three-fifth shaded circle.
Step 2:
$1 + 1 + \frac{3}{5} = 2\frac{3}{5}$
So, this combination of figures is represented by the mixed number $2\frac{3}{5}$.
Example 2
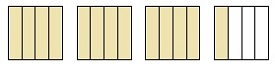
Write an improper fraction for the shaded region given below
Solution
Step 1:
There are three shaded whole rectangular strips and a one-fourth shaded strip.
Step 2:
$1 + 1 + 1 + \frac{1}{4} = 3\frac{1}{4}$
So, this combination of figures is represented by the mixed number $3\frac{1}{4}$
Step 3:
$3\frac{1}{4}$ is written as an improper fraction using an algorithm as follows.
$3\frac{1}{4} = \frac{\left ( 3 \times 4 + 1 \right )}{4} = \frac{13}{4}$
So, the improper fraction representing the given shaded region is $\frac{13}{4}$.