Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum sum path between two leaves of a binary trees in C++
Problem statement
Given a binary tree in which each node element contains a number. The task is to find the minimum possible sum from one leaf node to another.
Example
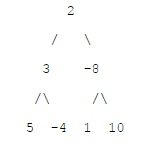
In above tree minimum sub path is -6 as follows: (-4) + 3 + 2 + (-8) + 1
Algorithm
The idea is to maintain two values in recursive calls −
- Minimum root to leaf path sum for the subtree rooted under current node
- The minimum path sum between leaves
- For every visited node X, we have to find the minimum root to leaf sum in left and right sub trees of X. Then add the two values with X’s data, and compare the sum with the current minimum path sum
Example
#include <bits/stdc++.h>
using namespace std;
typedef struct node {
int data;
struct node *left;
struct node *right;
} node;
node *newNode(int data) {
node *n = new node;
n->data = data;
n->left = NULL;
n->right = NULL;
return n;
}
int getMinPath(node *root, int &result) {
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return root->data;
}
int leftSum = getMinPath(root->left, result);
int rightSum = getMinPath(root->right, result);
if (root->left && root->right) {
result = min(result, root->data + leftSum + rightSum);
return min(root->data + leftSum, root->data + rightSum);
}
if (root->left == NULL) {
return root->data + rightSum;
} else {
return root->data + leftSum;
}
}
int getMinPath(node *root) {
int result = INT_MAX;
getMinPath(root, result);
return result;
}
node *createTree() {
node *root = newNode(2);
root->left = newNode(3);
root->right = newNode(-8);
root->left->left = newNode(5);
root->left->right = newNode(-4);
root->right->left = newNode(1);
root->right->right = newNode(10);
return root;
}
int main() {
node *root = createTree();
cout << "Minimum sum path = " << getMinPath(root) << endl;
return 0;
}When you compile and execute above program. It generates following output −
Output
Minimum sum path = -6
Updated on: 20-Dec-2019
126 Views
Advertisements