Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find sum of all left leaves in a given Binary Tree in C++
In this problem, we are given a binary tree. Our task is to find the sum of all left leaves in a given Binary Tree.
Let's take an example to understand the problem,
Input :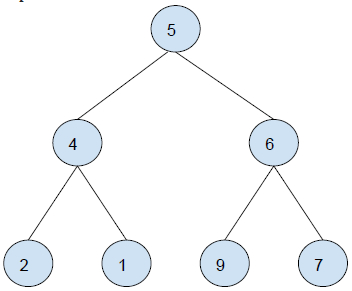 
Output : 11
Explanation −
All leaf nodes of the tree are : 2, 9 Sum = 2 + 9 = 11
Solution Approach
A simple solution to the problem is traversing the tree from root to leaf. If a node is a left leaf node, add it to sum. When the whole tree is traversed. Print Sum.
Example
Program to illustrate the working of our solution
#include <iostream>
using namespace std;
struct Node{
int key;
struct Node* left, *right;
};
Node *newNode(char k){
Node *node = new Node;
node->key = k;
node->right = node->left = NULL;
return node;
}
bool isLeafNode(Node *node){
if (node == NULL)
return false;
if (node->left == NULL && node->right == NULL)
return true;
return false;
}
int findLeftLeavesSum(Node *root){
int sum = 0;
if (root != NULL){
if (isLeafNode(root->left))
sum += root->left->key;
else
sum += findLeftLeavesSum(root->left);
sum += findLeftLeavesSum(root->right);
}
return sum;
}
int main(){
struct Node *root = newNode(5);
root->left = newNode(4);
root->right = newNode(6);
root->left->left = newNode(2);
root->left->right = newNode(1);
root->right->left = newNode(9);
root->right->right = newNode(7);
cout<<"The sum of left leaves of the tree is "<<findLeftLeavesSum(root);
return 0;
}Output
The sum of left leaves of the tree is 11
Another approach using Iteration
We will perform depth first search traversal on the tree, And then check if the current node is a left leaf. If Yes, add its value to sum, otherwise, leave. At the end, print the sum.
Example
Program to illustrate the working of our solution
#include<bits/stdc++.h>
using namespace std;
struct Node{
int key;
struct Node* left, *right;
};
Node *newNode(char k){
Node *node = new Node;
node->key = k;
node->right = node->left = NULL;
return node;
}
int findLeftLeavesSum(Node* root){
if(root == NULL)
return 0;
stack<Node*> treeNodes;
treeNodes.push(root);
int sum = 0;
while(treeNodes.size() > 0){
Node* currentNode = treeNodes.top();
treeNodes.pop();
if (currentNode->left != NULL){
treeNodes.push(currentNode->left);
if(currentNode->left->left == NULL &&
currentNode->left->right == NULL){
sum += currentNode->left->key ;
}
}
if (currentNode->right != NULL)
treeNodes.push(currentNode->right);
}
return sum;
}
int main(){
Node *root = newNode(5);
root->left= newNode(4);
root->right = newNode(6);
root->left->left = newNode(2);
root->left->right = newNode(1);
root->right->left = newNode(9);
root->right->right= newNode(7);
cout<<"The sum of left leaves of the tree is "<<findLeftLeavesSum(root);
return 0;
}Output
The sum of left leaves of the tree is 11
Approach 3, using BFS
We will perform a breadth first search with a variable to indicate whether the node is left child or not. If it is, add it to the sum, else leave. At the end, print sum.
Example
Program to illustrate the working of our solution
#include<bits/stdc++.h>
using namespace std;
struct Node{
int key; struct Node* left, *right;
};
Node *newNode(char k){
Node *node = new Node;
node->key = k;
node->right = node->left = NULL;
return node;
}
int findLeftLeavesSum(Node* root) {
if (root == NULL)
return 0;
queue<pair<Node*, bool> > leftTreeNodes;
leftTreeNodes.push({ root, 0 });
int sum = 0;
while (!leftTreeNodes.empty()) {
Node* temp = leftTreeNodes.front().first;
bool is_left_child = leftTreeNodes.front().second;
leftTreeNodes.pop();
if (!temp->left && !temp->right && is_left_child)
sum = sum + temp->key;
if (temp->left) {
leftTreeNodes.push({ temp->left, 1 });
}
if (temp->right) {
leftTreeNodes.push({ temp->right, 0 });
}
}
return sum;
}
int main(){
Node *root = newNode(5);
root->left= newNode(4);
root->right = newNode(6);
root->left->left = newNode(2);
root->left->right = newNode(1);
root->right->left = newNode(9);
root->right->right= newNode(7);
cout<<"The sum of left leaves of the tree is "<<findLeftLeavesSum(root);
return 0;
}Output
The sum of left leaves of the tree is 11
300 Views
To Continue Learning Please Login