Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum Cuts can be made in the Chessboard such that it is not divided into 2 parts in C++
Concept
Given A x B Chessboard, the task is to calculate the Maximum numbers of cuts that we can build in the Chessboard so that the Chessboard is not divided into 2 parts.
Examples
The examples are given below −
Input
A = 2, B = 4
Output
Number of maximum cuts = 3
Input
A = 2, B = 2
Output
Number of maximum cuts = 1
Method
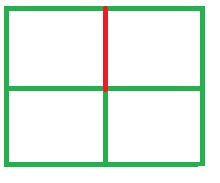
For A = 2, B = 2 ,we can only build 1 cut (mark in red). If we build 1 more cut then the chessboard will divide into 2 pieces
For A = 2, B = 4 ,we can makes 3 cuts (marks in red). If we build 1 more cut then the chessboard will divide into 2 pieces.
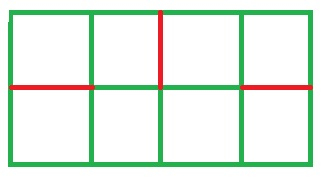
As a result of this, it can be observed that no. of cuts = (A-1) * (B-1).
Example
//This is C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;
// function that calculates the maximum no. of cuts
int numberOfCuts1(int A, int B){
int result1 = 0;
result1 = (A - 1) * (B - 1);
return result1;
}
// Driver Code
int main(){
int A = 4, B = 4;
// Calling function.
int Cuts = numberOfCuts1(A, B);
cout << "Maximum cuts = " << Cuts;
return 0;
}Output
Maximum cuts = 9
Updated on: 23-Jul-2020
116 Views
Advertisements