Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum bishops that can be placed on N*N chessboard in C++
We are given an input N which denotes the size of the chessboard. The task here is to find for any value of N, how many bishops can be placed on the NXN chessboard such that no two bishops can attack each other. Let’s understand with examples.
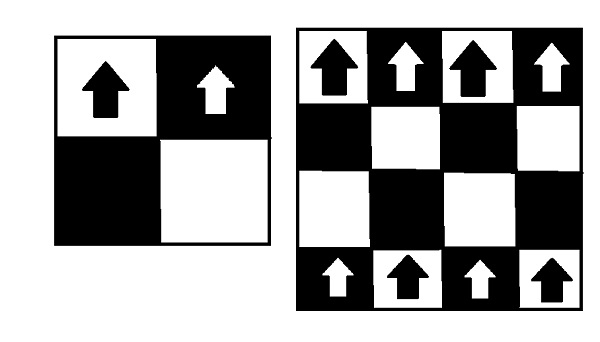
Input − N=2
Output− Maximum bishops that can be placed on N*N chessboard − 2 ( as shown above )
Explanation − As depicted above the only non-contradictory positions are where the bishops are placed. Bishops at-most for 2X2 chessboard.
Input − N=5
Output− Maximum bishops that can be placed on N*N chessboard: 8 ( as shown above )
Approach used in the below program is as follows
We take an integer value N as input for chessboard dimensions.
Pass this N as argument to totalBishops(int n).
For N<1 invalid input, bishops count=0.
For N=1, only 1 position, bishop count=1.
Else bishops will be 2*(N-1)
Store this result in variable bishops.
Return the result.
Example
#include <iostream>
//to return maximum bishops possible
int totalBishops(int n){
int bishops=0;
if (n < 1)
bishops= 0;
else if (n == 1)
bishops= 1;
else
bishops= 2 * (n - 1);
return bishops;
}
int main(){
int N = 15; //for chessboard dimensions N*N
printf("%d" ,totalBishops(N));
return 0;
}Output
If we run the above code it will generate the following output −
28
253 Views
