Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Mechanics of Train Movement and Derivation for Tractive Effort
Mechanism of Train Movement
The essential mechanism of an electric locomotive is shown in the figure below.
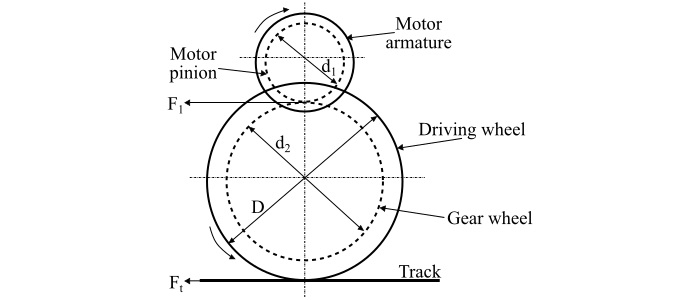
Here, the armature of the driving motor has a pinion of the diameter d1 attached to it. The tractive effort at the edge of the pinion is transferred to the driving wheel by means of a gearwheel.
Let,
T = Torque exterted by the motor in Nm
F1 = Tractive effort at the pinion
Ft = Tractive effort at the wheel
$\gamma $ = Gear ratio
d1 = Diameter of pinion
d2 = Diameter of gear wheel
D = Diameter of driving wheel
$\eta $ = Efficiency of power transmission from motor to driving axle
Hence, the torque exerted by the motor is given by,
$$\mathrm{\mathit{T}\:=\:\mathit{F_{\mathrm{1}}}\:\times \:\frac{\mathit{d_{\mathrm{1}}}}{2}}$$
$$\mathrm{\therefore \mathrm{Tractive\: effort\: at \:pinion,}\mathit{F_{\mathrm{1}}}\:=\:\frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{1} \right )}}$$
Now, the tractive effort transferred to the driving wheel is,
$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\eta \mathit{F_{\mathrm{1}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}\:=\:\eta \cdot \frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}}$$
$$\mathrm{\Rightarrow \mathit{F_{\mathit{t}}}\:=\:\eta \mathit{T}\mathrm{\left ( \frac{\mathrm{2}}{\mathit{D}} \right )}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}} \right )}}$$
$$\mathrm{\because \mathrm{Gear\:ratio,}\gamma\:=\: \:\frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}}}$$
$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\mathrm{2}\eta \gamma \mathrm{\left ( \frac{\mathit{T}}{\mathit{D}} \right )}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{2} \right )}}$$
Equation (2) gives the value of tractive effort at the driving wheel.
The maximum frictional force between the driving wheel and the track is equal to $\mu$W. Where, μ is the coefficient of adhesion between the driving wheel and the track and W is the weight of the train on the driving axles, known as adhesive weight. The adhesive weight is defined as the total weight to be carried on the driving wheels.
The slipping will not take place unless
$$\mathrm{\mathit{F_{t}}> \mu \mathrm{W}}$$
Therefore, for the motion of trains without slipping, the tractive effort should be less than or at the most equal to $\mu$W.
From the above discussion it is clear that the magnitude of the tractive effort that can be employed for propulsion of train depends upon the weight coming over the driving wheels and the coefficient of adhesion between the driving wheel and the track.
Coefficient of Adhesion
The coefficient of adhesion is defined as the ratio of the maximum tractive effort that can be applied without slipping of wheels to the adhesive weight, i.e.,
$$\mathrm{\mu \:=\:\frac{\mathrm{Maximum\: tractive\: effort\: that\: can\: be\: applied\: without\: slipping\: of\: wheels}}{\mathrm{Adhesive \:weight}}}$$
Also, the coefficient of adhesion decreases with the increase in speed. The normal value of the coefficient of adhesion with the clean and dry rails is 0.25 and with wet or greasy rails it is as low as 0.08.
Since the higher value of tractive effort can be used in electric traction so that the electric train can be made to accelerate at a faster rate. This results in saving of time, especially, when the distance between the stops is small.
Numerical Example
An electric train has eight motors geared to driving wheels, each wheel is 80 cm in diameter. Determine the torque developed by each motor to accelerate the train. The tractive effort required for accelerating the train to a speed of 50 kmph in 30 seconds is of 117590 N, the gear ratio is 4 to 1 and the gearing efficiency is 85%.
Solution
Given data,
Diameter of wheel,D = 80 cm = 0.8 m
Tractive effort, Ft = 117590 N
Gear ratio,$\gamma$ = 4
Gearing efficiency, $\eta$ = 85% = 0.85
Hence, the total torque developed by 8 motors is,
$$\mathrm{\mathit{T}\:=\:\frac{\mathit{F_{t}\times \mathit{D}}}{2\gamma \eta }\:=\:\frac{117590\times 0.8}{2\times 4\times 0.85}\:=\:13834.117\:\mathrm{NM}}$$
Therefore, the torque developed by each motor is,
$$\mathrm{\mathit{T_{\mathrm{each\:motor}}}\:=\:\frac{13834.117}{8}\:=\:1729.26\:\mathrm{NM}}$$
4K+ Views
