Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Tractive Effort for Propulsion of Train
What is Tractive Effort?
The effective force required for propelling a train at the wheel of locomotive is known as the tractive effort. It is denoted by 𝑭𝒕 and is measured in Newton. It is a vector quantity always acting tangential to the wheels of the locomotive.
Tractive Effort for Propulsion of Train
The total tractive effort required to propel the train on the track is equal to the sum of −
Tractive effort required for linear and angular acceleration (𝐹𝑎).
Tractive effort to overcome the effect of gravity (𝐹𝑔).
Tractive effort to overcome the train resistance (𝐹𝑟).
Therefore, the total tractive effort is given as,
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{g}\pm F_{r}}\; \cdot \cdot \cdot \left ( 1 \right )}$$
Tractive Effort for Linear and Angular Acceleration
According to the laws of dynamics, the force required to accelerate the motion of the body is given by,
$$\mathrm{Force,\mathit{F}\mathrm{\: =\: }Mass(\mathit{m})\times Acceleration(\alpha )}$$
Now, consider a train of weight W tons being accelerated at α kmphps, then,
$$\mathrm{Mass\: of\: train\mathrm{\: =\: }1000\mathit{W}\: kg}$$
$$\mathrm{Acceleration,\alpha \mathrm{\: =\: }\alpha \:kmphps\mathrm{\: =\: }\alpha \times \frac{1000}{3600}m/s^{2}\mathrm{\: =\: }0.2778\alpha \: m/s^{2} }$$
Therefore, the tractive effort required for linear acceleration is,
$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }m\alpha \mathrm{\: =\: }\mathrm{1000}W\times \mathrm{0.2778\alpha } \mathrm{\: =\: }\mathrm{277.8}W\alpha}\: Newtons}$$
With the linear acceleration of the train, the rotating parts of the train like wheels and motor shafts also accelerate in an angular direction. Therefore, the tractive effort required is equal to the arithmetic sum of tractive effort required to have the linear acceleration and the tractive effort required to have the angular acceleration of rotating parts.
Actually, the tractive effort required to have the angular acceleration depends upon the individual weight, radius of gyration, etc. of the rotating parts requiring angular acceleration. Thus, the equivalent accelerating weight of the train is taken as 𝑾𝒆 which is 8% to 15% higher than W.
Therefore, the tractive effort required for linear and angular acceleration is given by,
$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }}277.8\, \mathit{W_{e}\alpha}\: Newtons\; \; \cdot \cdot \cdot \left ( 2 \right )}$$
Tractive Effort for Overcoming the Effect of Gravity
When a train is on a gradient (or slope), a force of gravity equal to the component of the dead weight along the slope acts on the train and tends to cause its motion down. Therefore, the force due to gradient is given by,
$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }mg}\: sin\, \theta \mathrm{\: =\: } 1000 \mathit{W_{g}}\: sin\theta}$$
But, in railway work, the gradient is expressed as rise in meters in a track distance of 100 meters and is denoted as percentage gradient (G%). Now from the figure, we have,
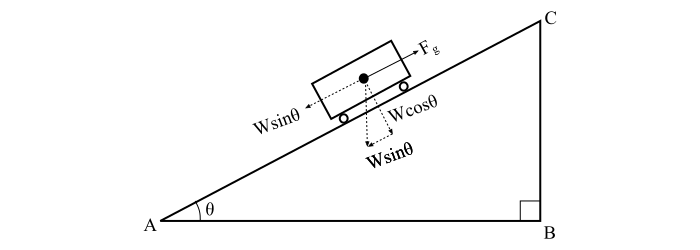
$$\mathrm{Slope\: or\: Gradient,G \mathrm{\: =\: } sin\, \theta \mathrm{\: =\: }\frac{Elelvation \, (BC)}{Distance\: along\: the\: track\: (AC)}}$$
$$\mathrm{\%G \mathrm{\: =\: } sin\, \theta \times 100}$$
$$\mathrm{\Rightarrow sin\, \theta \mathrm{\: =\: }\frac{\mathit{G}}{100}}$$
Therefore,
$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }\mathrm{1000}Wg\times \frac{\mathit{G}}{\mathrm{100}}}\mathrm{\: =\: }10\mathit{WG}\times 9.81}$$
$$\mathrm{\Rightarrow \mathit{F_{g}\mathrm{\: =\: } \mathrm{9.81}\mathit{WG}}\; Newton\; \; \cdot \cdot \cdot \left ( 3 \right )}$$
Where, g = 9.81 m/s2, acceleration due to gravity.
Tractive Effort Required for Overcoming Train Resistance
The train resistance consists of all the forces resisting the motion of a train when it is running at uniform speed on a straight and level track. Under these conditions, the entire energy output from the driving axles is expended against train resistance.
The train resistance is mainly due to −
The friction at the various parts of the rolling stock.
The friction at the track.
Air resistance.
Here, the first two components constitute the mechanical resistance component of the train resistance. Also, the train resistance depends upon various factors like shape, size and condition of the track, etc. and it is expressed in Newton per ton of the dead weight. For a normal train, the value of specific resistance varies from 40 to 70 N/ton.
Thus, the general expression for the train resistance is,
$$\mathit{R\mathrm{\: =\: }k_{\mathrm{1}}\mathrm{\: +\: }k_{\mathrm{2}}V\mathrm{\: +\: }k_{\mathrm{3}}V^{\mathrm{2}}}$$
Where, 𝑘1, 𝑘2 and 𝑘3 are the constants whose value depends upon the train and track. R is the resistance in Newton and V is the speed in kmph.
Hence, the tractive effort required to overcome the train resistance is
$$\mathit{F_{r}\mathrm{\: =\: }W\times r\; \; \cdot \cdot \cdot \mathrm{\left ( 4 \right )}}$$
Where, 𝒓 is the specific resistance per ton of the dead weight of train.
Therefore, on substituting the values from equations (2), (3) & (4) in eqn. (1), we get the total tractive effort required to run the train as,
$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{r}\mathrm{\: =\: }\mathrm{277.8}W_{e}\alpha \pm \mathrm{98.1}WG\mathrm{\: +\: }Wr}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$
Here, +ve sign is for the motion up the gradient and –ve sign for the motion down the gradient.
7K+ Views
