Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Maximum Binary Tree II in C++
Suppose we have a root node of a maximum tree: The maximum tree is a tree where every node has a value greater than any other value in its subtree. Suppose we have a method called construct(). This can construct a root from a list A. The construct() method is like −
If list A is empty, return null.
Otherwise, let A[i] be the largest element of the list A. Then create a root node with value A[i].
The left child of root will be construct([A[0], A[1], ..., A[i-1]])
The right child of root will be construct([A[i+1], A[i+2], ..., A[n - 1]]) [n is the length of A]
Return root.
Note that we were not given A directly, only a root node root = construct(A). Now suppose B is a copy of A with the value val added to it. It is guaranteed that B has unique values. We have to construct(B). If value is 5 and the input tree is like −
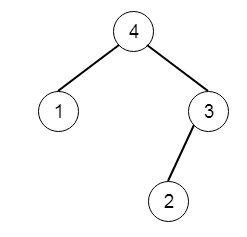
The output tree is like −
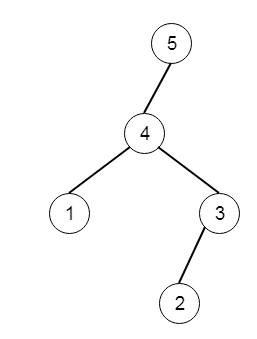
To solve this, we will follow these steps −
define one recursive method solve(). This is taking root and val
If tree is empty, then create a new node with value val, and return that node
if value of root < val, then
temp := new node whose value is val
left of temp := root
return temp
right of root := solve(right of root, val)
return root
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
class TreeNode{
public:
int val;
TreeNode *left, *right;
TreeNode(int data){
val = data;
left = NULL;
right = NULL;
}
};
void insert(TreeNode **root, int val){
queue<TreeNode*> q;
q.push(*root);
while(q.size()){
TreeNode *temp = q.front();
q.pop();
if(!temp->left){
if(val != NULL)
temp->left = new TreeNode(val);
else
temp->left = new TreeNode(0);
return;
}else{
q.push(temp->left);
}
if(!temp->right){
if(val != NULL)
temp->right = new TreeNode(val);
else
temp->right = new TreeNode(0);
return;
}else{
q.push(temp->right);
}
}
}
TreeNode *make_tree(vector<int> v){
TreeNode *root = new TreeNode(v[0]);
for(int i = 1; i<v.size(); i++){
insert(&root, v[i]);
}
return root;
}
void tree_level_trav(TreeNode*root){
if (root == NULL) return;
cout << "[";
queue<TreeNode *> q;
TreeNode *curr;
q.push(root);
q.push(NULL);
while (q.size() > 1) {
curr = q.front();
q.pop();
if (curr == NULL){
q.push(NULL);
}
else {
if(curr->left)
q.push(curr->left);
if(curr->right)
q.push(curr->right);
if(curr == NULL || curr->val == 0){
cout << "null" << ", ";
}else{
cout << curr->val << ", ";
}
}
}
cout << "]"<<endl;
}
class Solution {
public:
TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
if(!root)return new TreeNode(val);
if(root->val < val){
TreeNode* temp = new TreeNode(val);
temp->left = root;
return temp;
}
root->right = insertIntoMaxTree(root->right, val);
return root;
}
};
main(){
vector<int> v = {4,1,3,NULL,NULL,2};
TreeNode *root = make_tree(v);
Solution ob;
tree_level_trav(ob.insertIntoMaxTree(root, 5));
}Input
[4,1,3,null,null,2] 5
Output
[5, 4, 1, 3, null, null, 2, ]
94 Views
