Maximize a Value for a Semicircle of a given Radius

What do understand by the question embedded in the title i.e Maximize a value for a semicircle of a given radius?

The title `Maximize a value for a semicircle of a given radius` sounds unclear. Isn’t it? Let’s discuss what it means in the article below:

According to the title, If we have a semicircle with radius R, we need to find the maximum value of the expression F = PS^2 + PQ, where P is a point on the circumference of the semicircle, and PQ and PS are the two segments connecting P to the two endpoints of the diameter. Still confused, have a look at the diagram below and then try to understand.

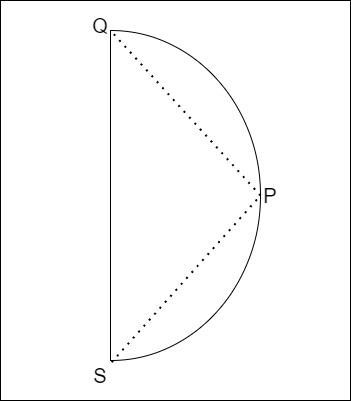
Are you able to understand the question now? Cool, now let's move to the logic we need to implement to solve it.

If you take a close look at the diagram, you will notice that triangle PQS will always be a right−angled triangle, regardless of the position of point P on the circumference of the circle.

So, as PQS is right−angled, we can use the Pythagorean theorem to relate the sides of this triangle as follows:

QS^2 = PQ^2 + PS^2 (h^2= b^2+p^2)

Since QS is the diameter of the semicircle, we know that QS = 2R. Substituting this into the above equation, we get:

4R^2 = PQ^2 + PS^2

• We can rearrange this equation as follows: PS^2 = 4R^2 − PQ^2

• We can substitute this expression for PS^2 into the expression for F, to get:F = 4R^2 − PQ^2 + PQ

Now moving to the next step, you might have learned about maxima and minima. To find the maximum value of F, we can use the concept of maxima and minima. We differentiate F with respect to PQ and set the derivative equal to zero to find the critical point(s) of F.

dF/dPQ = −2PQ + 1

• Setting this derivative equal to zero, we get: −2PQ + 1 = 0

• Solving for PQ, we get: PQ = ½

• Substituting this value of PQ into the expression for F, we get:

F = 4R^2 + 1/4

Therefore, the maximum value of F is 4R^2 + 1/4, which occurs when PQ = 1/2. This maximum value is independent of the position of point P on the circumference of the semicircle.

Approach

Having discussed the logic which goes into solving the problem, let’s discuss the step−by−step approach to convert the above logic into working code.

• We will take in the radius of the semi−circle as input.

• Now, we will use the formula concluded above to calculate the maximum value (4R^2 + 1/4)

• Now we will print the maximum value to the console.

C++ Code Implementation

Too much theory? Now, we have the logic and the approach, let’s convert them into working code. Here is the c++ code implementation to Maximize a value for a semicircle of the given radius.

Example

#include <iostream>
#include <cmath>
using namespace std;double findMaxF(double R) {    
   double F = 4 * R * R + 1.0 / 4.0;    
   return F;
}
int main() {    
   double R = 3.5;    
   double maxF = findMaxF(R);    
   cout << "The maximum value of F is: " << maxF << endl;    
   return 0;
}

Output

The maximum value of F is: 49.25

Time Complexity: O(1)

Space Complexity: O(1)

Conclusion

In this article, we have covered the logic behind the program to Maximize a value for a semicircle of a given radius. Hope you had a clear idea of the concept now.