Area of a n-sided regular polygon with given Radius?

Here we will see how to get the area of an n-sided regular polygon whose radius is given. Here the radius is the distance from the center of any vertex. To solve this problem, we have drawn one perpendicular from the center to one side. Let each side is of length ‘a’. The perpendicular is dividing the side into two parts. The length of each part is a/2. The perpendicular and one radius is making an angle x. Let the length of the radius is h.

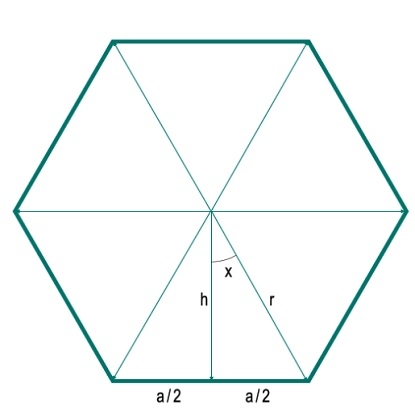
Here we can see that the polygon is divided into N equal triangles. So for any polygon with N sides, will be divided into N triangles. So the angle at the center is 360. That is divided into 360°/N different angles (Here 360°/6 = 60°). So the angle x is 180°/N. Now we can easily get the h and a using trigonometric equations.

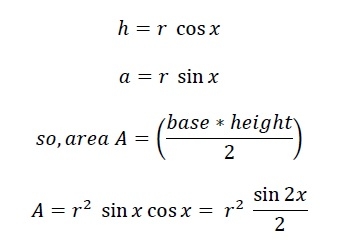
Now the area of whole polygon is N*A.

Example

#include <iostream>
#include <cmath>
using namespace std;
float polygonArea(float r, int n){
   return ((r * r * n) * sin((360 / n) * 3.1415 / 180)) / 2; //convert
   angle to rad then calculate
}
int main() {
   float rad = 9.0f;
   int sides = 6;
   cout << "Polygon Area: " << polygonArea(rad, sides);
}

Output

Polygon Area: 210.44