
- ML - Home
- ML - Introduction
- ML - Getting Started
- ML - Basic Concepts
- ML - Ecosystem
- ML - Python Libraries
- ML - Applications
- ML - Life Cycle
- ML - Required Skills
- ML - Implementation
- ML - Challenges & Common Issues
- ML - Limitations
- ML - Reallife Examples
- ML - Data Structure
- ML - Mathematics
- ML - Artificial Intelligence
- ML - Neural Networks
- ML - Deep Learning
- ML - Getting Datasets
- ML - Categorical Data
- ML - Data Loading
- ML - Data Understanding
- ML - Data Preparation
- ML - Models
- ML - Supervised Learning
- ML - Unsupervised Learning
- ML - Semi-supervised Learning
- ML - Reinforcement Learning
- ML - Supervised vs. Unsupervised
Machine Learning Data Visualization
- ML - Data Visualization
- ML - Histograms
- ML - Density Plots
- ML - Box and Whisker Plots
- ML - Correlation Matrix Plots
- ML - Scatter Matrix Plots
Statistics for Machine Learning
- ML - Statistics
- ML - Mean, Median, Mode
- ML - Standard Deviation
- ML - Percentiles
- ML - Data Distribution
- ML - Skewness and Kurtosis
- ML - Bias and Variance
- ML - Hypothesis
Regression Analysis In ML
- ML - Regression Analysis
- ML - Linear Regression
- ML - Simple Linear Regression
- ML - Multiple Linear Regression
- ML - Polynomial Regression
- ML - Classification Algorithms
- ML - Logistic Regression
- ML - K-Nearest Neighbors (KNN)
- ML - Naïve Bayes Algorithm
- ML - Decision Tree Algorithm
- ML - Support Vector Machine
- ML - Random Forest
- ML - Confusion Matrix
- ML - Stochastic Gradient Descent
- ML - Clustering Algorithms
- ML - Centroid-Based Clustering
- ML - K-Means Clustering
- ML - K-Medoids Clustering
- ML - Mean-Shift Clustering
- ML - Hierarchical Clustering
- ML - Density-Based Clustering
- ML - DBSCAN Clustering
- ML - OPTICS Clustering
- ML - HDBSCAN Clustering
- ML - BIRCH Clustering
- ML - Affinity Propagation
- ML - Distribution-Based Clustering
- ML - Agglomerative Clustering
- ML - Dimensionality Reduction
- ML - Feature Selection
- ML - Feature Extraction
- ML - Backward Elimination
- ML - Forward Feature Construction
- ML - High Correlation Filter
- ML - Low Variance Filter
- ML - Missing Values Ratio
- ML - Principal Component Analysis
- ML - Reinforcement Learning Algorithms
- ML - Exploitation & Exploration
- ML - Q-Learning
- ML - REINFORCE Algorithm
- ML - SARSA Reinforcement Learning
- ML - Actor-critic Method
- ML - Monte Carlo Methods
- ML - Temporal Difference
- ML - Deep Reinforcement Learning
- ML - Deep Reinforcement Learning Algorithms
- ML - Deep Q-Networks
- ML - Deep Deterministic Policy Gradient
- ML - Trust Region Methods
- ML - Performance Metrics
- ML - Automatic Workflows
- ML - Boost Model Performance
- ML - Gradient Boosting
- ML - Bootstrap Aggregation (Bagging)
- ML - Cross Validation
- ML - AUC-ROC Curve
- ML - Grid Search
- ML - Data Scaling
- ML - Train and Test
- ML - Association Rules
- ML - Apriori Algorithm
- ML - Gaussian Discriminant Analysis
- ML - Cost Function
- ML - Bayes Theorem
- ML - Precision and Recall
- ML - Adversarial
- ML - Stacking
- ML - Epoch
- ML - Perceptron
- ML - Regularization
- ML - Overfitting
- ML - P-value
- ML - Entropy
- ML - MLOps
- ML - Data Leakage
- ML - Monetizing Machine Learning
- ML - Types of Data
Classification Algorithms In ML
Clustering Algorithms In ML
Dimensionality Reduction In ML
Reinforcement Learning
Deep Reinforcement Learning
Quantum Machine Learning
Machine Learning Miscellaneous
Machine Learning - Resources
Machine Learning - Confusion Matrix
What is Confusion Matrix?
The confusion matrix in machine learning is the easiest way to measure the performance of a classification problem where the output can be of two or more type of classes. It is nothing but a table with two dimensions viz. "Actual" and "Predicted" and furthermore, both the dimensions have "True Positives (TP)", "True Negatives (TN)", "False Positives (FP)", "False Negatives (FN)" as shown below −
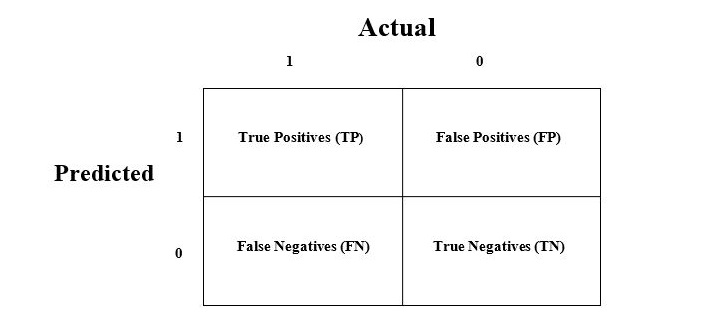
Take an example of classifying emails as "spam" and "not spam" for a better understanding. Here a spam email is labeled as "positive" and a legitimate (not spam) email is labeled as negative.
Explanation of the terms associated with confusion matrix are as follows −
True Positives (TP) − It is the case when both actual class & predicted class of data point is 1. The classification model correctly predicts the positive class label for data sample. For example, a "spam" email is classified as "spam".
True Negatives (TN) − It is the case when both actual class & predicted class of data point is 0. The model correctly predicts the negative class label for data sample. For example, a "not spam" email is classified as "not spam".
False Positives (FP) − It is the case when actual class of data point is 0 & predicted class of data point is 1. The model incorrectly predicts the positive class label for data sample. For example, a "not spam" email is misclassified as "spam". It is known as a Type I error.
False Negatives (FN) − It is the case when actual class of data point is 1 & predicted class of data point is 0. The model incorrectly predicts the negative class label for data sample. For example, a "spam" email is misclassified as "not spam". It is also known as Type II error.
We use the confusion matrix to find correct and incorrect classifications −
- Correct classification − TP and TN are correctly classified data points.
- Incorrect classification − FP and FN are incorrectly classified data points.
We can use the confusion matrix to calculate different classification metrics such as accuracy, precision, recall, etc. But before discussing these metrics, let's take understand how to create a confusion matrix with the help of a practical exmaple.
Confusion Matrix Practical Example
Let's take a practical example for a classifications of emails as "spam" or "not spam". Here we are representing class for a spam email as positive (1) and a not spam email as negative (0). So emails are classified either −
- spam (1) − positive class lebel
- not spam (0) − negative class lebel
The actual and predicted classes/ categories are as follows −
| Actual Classification | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| Predicted Classification | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
So with the above results, let's find out that a particular classification falls under TP, TN, FP or FN. Look at the below table −
| Actual Classification | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| Predicted Classification | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| Result | TN | TP | TN | TP | FN | FP | TN | FN | TP | TP |
In above table, when we compare actual classification set to the predicted classification, we observe that there are four different types of outcomes. First, true positive (1,1), i.e. the actual classification is positive and predicted classification is also postive. This means the classifier has identified postive sample correctly. Second, false negative (1,0), i.e., the actual classification is positive and predicted classification in negative. The classifier has identified positive sample as negative.
Third, false positive, (0,1), i.e., the actual classification is negative and predicted classification is postive. The negative sample is incorrectly identified as positive. Fourth, true negative (0,0), i.e., the actual and predicted classifications are negative. The negative sample is correctly identified by model as negative.
Let's find the total number of samples in each categories.
- TP (True Positive): 4
- FN (False Negative): 2
- FP (False Positive): 1
- TN (True Negative): 3
Let's now create confusion matrix as following −
| Actual Class | |||
| Positive (1) | Negative (0) | ||
|
Predicted Class
|
Positive (1) | 4 (TP) | 1 (FP) |
| Negative (0) | 2 (FN) | 3 (TN) | |
So far we have created the confusion matrix for above problem. Let's infer some meaning from the above matrix −
- Amongst 10 emails, four "spam" emails are correctly classified as "spam" (TP).
- Amongst 10 emails, two "spam" emails are incorrectly classified as "not spam" (FN).
- Amongst 10 emails, one "not spam" email is incorrectly classified as "spam" (FP).
- Amongst 1o emails, three "not spam" emails are correctly classified as "not spam" (TN).
- So Amongst 10 emails, seven emails are correctly classified (TP & TN)and three emails are incorrectly classified (FP & FN).
Classificaiton Metrics Based on Confusion Matrix
We can define many classificaiton performance metrics using the confusion matrix. We will consider the above practical example and calculate the metrics using the values in that example. Some of them are as follows −
- Accuracy
- Precision
- Recall or Sensitivity
- Specificity
- F1 Score
- Type I Error Rate
- Type II Error Rate
Accuracy
Accuracy is most common metrics to evaluate a classification model. It is ratio of total correction predictions and all predictions made. Mathematically we can use the following formula to calculate accurcy −
$$\mathrm{Accuracy = \frac{TP + TN}{TP + FP + FN + TN}}$$
Let's calculate the accuracy −
$$\mathrm{Accuracy = \frac{4 + 3}{4 + 1 + 2 + 3}= \frac{7}{10} = 0.7}$$
Hence the model's classification accuracy is 70%.
Precision
Precision measures the proportion of true positive instances out of all predicted positive instances. It is calculated as ratio of the number of true positive instances and the sum of true positive and false positive instances.
$$\mathrm{Precision = \frac{TP}{TP + FP}}$$
Let's calculate the precision −
$$\mathrm{Precision = \frac{4}{4 + 1} = \frac{4}{5} = 0.8}$$
Recall or Sensitivity
Recall (Sensitivity) is defined as the number of positives classifications by the classifier. We can calculate it with the help of following formula
$$\mathrm{Recall = \frac{TP}{TP + FN}}$$
Let's calculate recall −
$$\mathrm{Recall = \frac{4}{4 + 2} = \frac{4}{6} = 0.666}$$
Specificity
Specificity, in contrast to recall, is defined as the number of negatives returned by the classifier. We can calculate it with the help of following formula −
$$\mathrm{Specificity = \frac{TN}{TN + FP}}$$
Let's calculate the specificity −
$$\mathrm{Specificity = \frac{3}{3 + 1} = \frac{3}{4} = 0.75}$$
F1 Score
F1 score is a balanced measure that takes into account both precision and recall. It is the harmonic mean of precision and recall.
We can calculate F1 score with the help of following formula −
$$\mathrm{F1 \: Score = 2 \times \frac{(Precision \times Recall)}{Precision + Recall}}$$
Let's calculate F1 score −
$$\mathrm{F1 \: Score = 2 \times \frac{(0.8 \times 0.667)}{0.8 + 0.667} = 0.727}$$
Hence, F1 score is 0.727.
Type I Error Rate
Type I error occurs when the classifier predicts positive classification but it is actually negative class. The type I error rate is calculated as −
$$\mathrm{Type \: I \: Error \: Rate = \frac{FP}{FP + TN}}$$
$$\mathrm{Type \: I \: Error \: Rate = \frac{1}{1 + 3} = \frac{1}{4} = 0.25}$$
Type II Error Rate
Type II error occurs when the classifier predicts negative but it is actually positive class. The type II error rate can be calculate as −
$$\mathrm{Type \: II \: Error \: Rate = \frac{FN}{FN + TP}}$$
$$\mathrm{Type \: II \: Error \: Rate = \frac{2}{2 + 4} = \frac{2}{6} = 0.333}$$
How to Implement Confusion Matrix in Python?
To implement the confusion matrix in Python, we can use the confusion_matrix() function from the sklearn.metrics module of the scikit-learn library.
Note: Please note that the confusion_matrix() function returns a 2D array that correspondence to the following confusion matrix −
| Predicted Class | |||
| Negative (0) | Positive (1) | ||
|
Actual Class
|
Negative (0) | True Negative (TN) | False Positive (FP) |
| Positive (1) | False Negative (FN) | True Positive (TP) | |
Here is an simple example of how to use the confusion_matrix() function −
from sklearn.metrics import confusion_matrix # Actual values y_actual = [0, 1, 0, 1, 1, 0, 0, 1, 1, 1] # Predicted values y_pred = [0, 1, 0, 1, 0, 1, 0, 0, 1, 1] # Confusion matrix cm = confusion_matrix(y_actual, y_pred) print(cm)
In this example, we have two arrays: y_actual contains the actual values of the target variable, and y_pred contains the predicted values of the target variable. We then call the confusion_matrix() function, passing in y_actual and y_pred as arguments. The function returns a 2D array that represents the confusion matrix.
The output of the code above will look like this −
[[3 1] [2 4]]
Compare the above result with the confusion matrix we created above.
- True Negative (TN): 3
- False Positive (FP): 1
- False Negative (FN): 2
- True Positive (TP): 4
We can also visualize the confusion matrix using a heatmap. Below is how we can do that using the heatmap() function from the seaborn library
import seaborn as sns # Plot confusion matrix as heatmap sns.heatmap(cm, annot=True, cmap='summer')
Output
This will produce a heatmap that shows the confusion matrix −
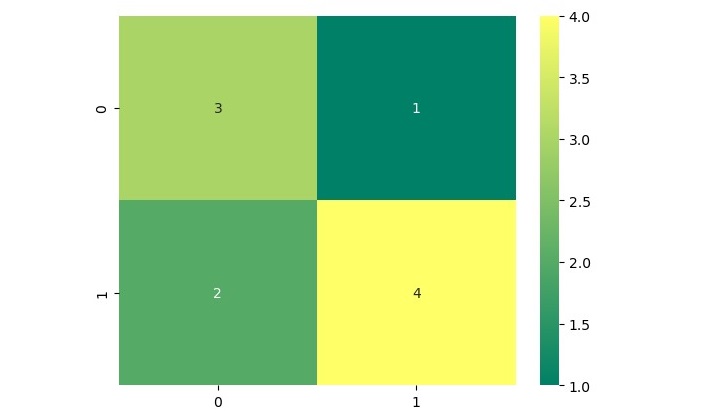
In this heatmap, the x-axis represents the predicted values, and the y-axis represents the actual values. The color of each square in the heatmap indicates the number of samples that fall into each category.