
- LISP Tutorial
- LISP - Home
- LISP - Overview
- LISP - Environment
- LISP - REPL
- LISP - Program Structure
- LISP - Basic Syntax
- LISP - Data Types
- Lisp Macros
- LISP - Macros
- LISP - Backquote and Comma
- LISP - Code Generation Using Macro
- LISP - Variable Capture and Hygienic macro
- LISP - Scope and Binding
- LISP - Macro Writing Style
- LISP - Macro Characters
- LISP - Read-Time Macros
- LISP - Compiler Macros
- LISP - Uses of Macros
- Lisp Functions
- LISP - Functions
- LISP - Functions vs Macros
- LISP - Calling Function using funcall
- LISP - Calling Function using apply
- LISP - Closures
- LISP - Functions as Arguments
- LISP - Functions as Return Values
- LISP - Recursion
- LISP - Built-in Functions
- Lisp Predicates
- LISP - Predicates
- LISP - Generic Data Type Predicates
- LISP - Specific Data Type Predicates
- LISP - Equality Predicates
- LISP - Numeric Predicates
- LISP - Comparison Predicates
- LISP - Logical Predicates
- LISP - List Predicates
- LISP - Custom Predicates
- LISP - Chaining Predicates
- Lisp Arrays
- LISP - Arrays
- LISP - Adjustable Arrays
- LISP - Fill Pointers in Arrays
- LISP - Specialized Arrays
- LISP - Arrays Properties
- LISP - Iterating over Arrays
- LISP - Multidimensional Arrays
- LISP - Row-Major Order
- Lisp Strings
- LISP - Strings
- LISP - String Concatenation
- LISP - String Comparison
- LISP - String Case Conversion
- LISP - String Trimmimg
- LISP - String Searching
- LISP - Getting Substring
- LISP - String Replacement
- LISP - Sorting Strings
- LISP - Merging Strings
- LISP - Accessing Characters of String
- LISP - String length
- LISP - Escape Sequences
- Lisp Sequences
- LISP - Sequences
- LISP - Accessing Element of Sequence
- LISP - Sequence length
- LISP - Getting Subsequence
- LISP - Search Element in Sequence
- LISP - Sequence Concatenation
- LISP - Reversing a Sequence
- LISP - Mapping Sequence Element
- LISP - position of Element
- LISP - Remove an Element
- LISP - Sort Sequence
- LISP - Merge Sequences
- LISP - every function
- LISP - some function
- LISP - notany function
- LISP - notevery function
- Lisp Lists
- LISP - Lists
- LISP - Accessing Elements of Lists
- LISP - Modifications to Lists
- LISP - Using mapcar on List
- LISP - Using mapc on List
- LISP - Using reduce on List
- LISP - Removing elements from List
- LISP - Reversing a List
- LISP - Sorting a List
- LISP - Searching a List
- LISP - List vs Vectors
- LISP - Matrix Multiplication
- Lisp Vectors
- LISP - Vectors
- LISP - Creating Vectors
- LISP - Accessing Elements of Vectors
- LISP - Modifications to Vectors
- LISP - Adjustable Vectors
- LISP - Specialized Vectors
- LISP - Vector Functions
- Lisp Set
- LISP - Set
- LISP - Adding elements to the Set
- LISP - Getting SubSet from a Set
- LISP - Set Difference
- LISP - Set Exclusive OR
- LISP - Set Intersection
- LISP - Set Union
- LISP - Representing Set with HashTable
- LISP - List as Set vs HashTable as Set
- Lisp Tree
- LISP - Tree
- LISP - Recursive Traversal
- LISP - Inorder Traversal
- LISP - Preorder Traversal
- LISP - Postorder Traversal
- LISP - Depth First Traversal
- LISP - Modifying Tree
- LISP - Search Tree
- LISP - Binary Tree
- Lisp Hash Table
- LISP - Hash Table
- Adding Values to Hash Table
- Removing Values from Hash Table
- Updating Values of Hash Table
- Iterating Hash Table Entries
- Searching key in HashTable
- Checking Size of HashTable
- Using Custom Equality Check
- Lisp - Input − Output
- LISP - Input − Output
- LISP - Streams
- LISP - Reading Data from Streams
- LISP - Writing Data to Streams
- LISP - File I/O
- LISP - String I/O
- LISP - Formatting with Format
- LISP - Interactive I/O
- LISP - Error Handling
- LISP - Binary I/O
- Lisp - Structures
- LISP - Structures
- LISP - Accessors and Mutators
- LISP - Structure Options
- LISP - Structure Types
- LISP - Applications and Best Practices
- Lisp - CLOS
- LISP - CLOS
- Lisp - Objects
- LISP - Class
- LISP - Slots and Accessors
- LISP - Generic Functions
- LISP - Class Precedence
- LISP - Metaobject Protocol
- LISP - Multimethods
- LISP - Multiple Inheritance
- LISP - Method Combinations
- LISP - Method Combinations
- LISP - :before Method Combination
- LISP - :primary Method Combination
- LISP - :after Method Combination
- LISP - :around Method Combination
- LISP - + Method Combination
- LISP - and Method Combination
- LISP - append Method Combination
- LISP Useful Resources
- Lisp - Quick Guide
- Lisp - Useful Resources
- Lisp - Discussion
Lisp - Tree
You can build tree data structures from cons cells, as lists of lists.
To implement tree structures, you will have to design functionalities that would traverse through the cons cells, in specific order, for example, pre-order, in-order, and post-order for binary trees.
Tree as List of Lists
Let us consider a tree structure made up of cons cell that form the following list of lists −
((1 2) (3 4) (5 6)).
Diagrammatically, it could be expressed as −
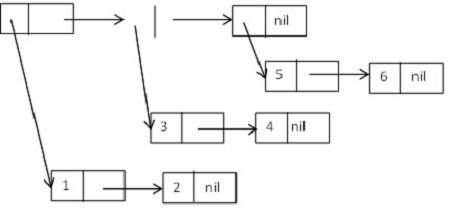
Tree Functions in LISP
Although mostly you will need to write your own tree-functionalities according to your specific need, LISP provides some tree functions that you can use.
Apart from all the list functions, the following functions work especially on tree structures −
| Sr.No. | Function & Description |
|---|---|
| 1 | copy-tree x & optional vecp It returns a copy of the tree of cons cells x. It recursively copies both the car and the cdr directions. If x is not a cons cell, the function simply returns x unchanged. If the optional vecp argument is true, this function copies vectors (recursively) as well as cons cells. |
| 2 | tree-equal x y & key :test :test-not :key It compares two trees of cons cells. If x and y are both cons cells, their cars and cdrs are compared recursively. If neither x nor y is a cons cell, they are compared by eql, or according to the specified test. The :key function, if specified, is applied to the elements of both trees. |
| 3 | subst new old tree & key :test :test-not :key It substitutes occurrences of given old item with new item, in tree, which is a tree of cons cells. |
| 4 | nsubst new old tree & key :test :test-not :key It works same as subst, but it destroys the original tree. |
| 5 | sublis alist tree & key :test :test-not :key It works like subst, except that it takes an association list alist of old-new pairs. Each element of the tree (after applying the :key function, if any), is compared with the cars of alist; if it matches, it is replaced by the corresponding cdr. |
| 6 | nsublis alist tree & key :test :test-not :key It works same as sublis, but a destructive version. |
Example
Create a new source code file named main.lisp and type the following code in it.
main.lisp
; create and set a list to lst (setq lst (list '(1 2) '(3 4) '(5 6))) ; copy and set a list to mylst (setq mylst (copy-list lst)) ; copy tree and set to tr (setq tr (copy-tree lst)) ; print the first list (write lst) ; terminate printing (terpri) ; print the second list (write mylst) ; terminate printing (terpri) ; print tree (write tr)
Output
When you execute the code, it returns the following result −
((1 2) (3 4) (5 6)) ((1 2) (3 4) (5 6)) ((1 2) (3 4) (5 6))
Example
Create a new source code file named main.lisp and type the following code in it.
main.lisp
; set a tree to tr (setq tr '((1 2 (3 4 5) ((7 8) (7 8 9))))) ; print tree (write tr) ; set trs as subtree (setq trs (subst 7 1 tr)) ; terminate printing (terpri) ; print tree (write trs)
Output
When you execute the code, it returns the following result −
((1 2 (3 4 5) ((7 8) (7 8 9)))) ((7 2 (3 4 5) ((7 8) (7 8 9))))
Building Your Own Tree
Let us try to build our own tree, using the list functions available in LISP.
First let us create a new node that contains some data
; define a function to create a tree node with an item (defun make-tree (item) "it creates a new node with item." (cons (cons item nil) nil) )
Next let us add a child node into the tree - it will take two tree nodes and add the second tree as the child of the first.
; define a function to add a tree node to the tree (defun add-child (tree child) (setf (car tree) (append (car tree) child)) tree)
This function will return the first child a given tree - it will take a tree node and return the first child of that node, or nil, if this node does not have any child node.
; define a function to get first child of the tree
(defun first-child (tree)
(if (null tree)
nil
(cdr (car tree))
)
)
This function will return the next sibling of a given node - it takes a tree node as argument, and returns a reference to the next sibling node, or nil, if the node does not have any.
; define a function to get sibling of the tree (defun next-sibling (tree) (cdr tree) )
Lastly we need a function to return the information in a node −
; define a function to get the data of a tree node (defun data (tree) (car (car tree)) )
Example
This example uses the above functionalities −
Create a new source code file named main.lisp and type the following code in it.
main.lisp
; define a function to create a tree
(defun make-tree (item)
"it creates a new node with item."
(cons (cons item nil) nil)
)
; create a function first child of a tree
(defun first-child (tree)
(if (null tree)
nil
(cdr (car tree))
)
)
; define a function to get sibling of a tree node
(defun next-sibling (tree)
(cdr tree)
)
; define a function to get details from a tree node
(defun data (tree)
(car (car tree))
)
; define a function to add a child to a tree node
(defun add-child (tree child)
(setf (car tree) (append (car tree) child))
tree
)
; set a tree
(setq tr '((1 2 (3 4 5) ((7 8) (7 8 9)))))
; create a tree and assign to mytree
(setq mytree (make-tree 10))
; print detail stored in a tree node
(write (data mytree))
; terminate printing
(terpri)
; print first child of tree
(write (first-child tr))
; terminate printing
(terpri)
; add a child to tree
(setq newtree (add-child tr mytree))
; terminate printing
(terpri)
; print tree
(write newtree)
Output
When you execute the code, it returns the following result −
10 (2 (3 4 5) ((7 8) (7 8 9))) ((1 2 (3 4 5) ((7 8) (7 8 9)) (10)))