LISP - Symbols

Lisp - Numbers

Quiz

Common Lisp defines several kinds of numbers. The number data type includes various kinds of numbers supported by LISP.

The number types supported by LISP are −

Integers
Ratios
Floating-point numbers
Complex numbers

The following diagram shows the number hierarchy and various numeric data types available in LISP −

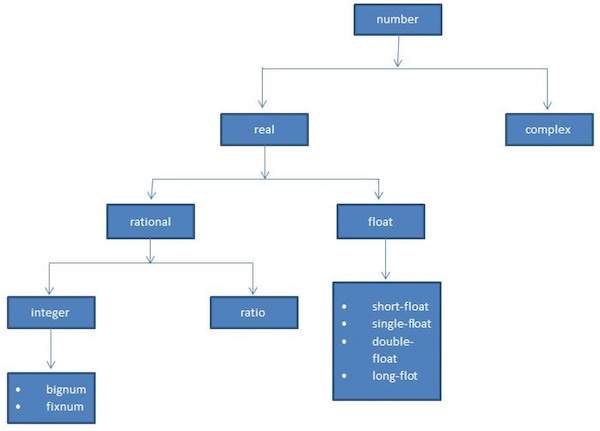
Various Numeric Types in LISP

The following table describes various number type data available in LISP −

Sr.No.	Data type & Description
1	fixnum This data type represents integers which are not too large and mostly in the range -215 to 215-1 (it is machine-dependent)
2	bignum These are very large numbers with size limited by the amount of memory allocated for LISP, they are not fixnum numbers.
3	ratio Represents the ratio of two numbers in the numerator/denominator form. The / function always produce the result in ratios, when its arguments are integers.
4	float It represents non-integer numbers. There are four float data types with increasing precision.
5	complex It represents complex numbers, which are denoted by #c. The real and imaginary parts could be both either rational or floating point numbers.

Example

Create a new source code file named main.lisp and type the following code in it.

main.lisp

; write 1/2
(write (/ 1 2))
; terminate printing
(terpri)
; execute and print the expression result
(write ( + (/ 1 2) (/ 3 4)))
; terminate printing
(terpri)
; execute and print the expression result
(write ( + #c( 1 2) #c( 3 -4)))

Output

When you execute the code, it returns the following result −

1/2
5/4
#C(4 -2)

Number Functions

The following table describes some commonly used numeric functions −

Sr.No.	Function & Description
1	*+, -, , /** Respective arithmetic operations
2	sin, cos, tan, acos, asin, atan Respective trigonometric functions.
3	sinh, cosh, tanh, acosh, asinh, atanh Respective hyperbolic functions.
4	exp Exponentiation function. Calculates e^x
5	expt Exponentiation function, takes base and power both.
6	sqrt It calculates the square root of a number.
7	log Logarithmic function. It one parameter is given, then it calculates its natural logarithm, otherwise the second parameter is used as base.
8	conjugate It calculates the complex conjugate of a number. In case of a real number, it returns the number itself.
9	abs It returns the absolute value (or magnitude) of a number.
10	gcd It calculates the greatest common divisor of the given numbers.
11	lcm It calculates the least common multiple of the given numbers.
12	isqrt It gives the greatest integer less than or equal to the exact square root of a given natural number.
13	floor, ceiling, truncate, round All these functions take two arguments as a number and returns the quotient; floor returns the largest integer that is not greater than ratio, ceiling chooses the smaller integer that is larger than ratio, truncate chooses the integer of the same sign as ratio with the largest absolute value that is less than absolute value of ratio, and round chooses an integer that is closest to ratio.
14	ffloor, fceiling, ftruncate, fround Does the same as above, but returns the quotient as a floating point number.
15	mod, rem Returns the remainder in a division operation.
16	float Converts a real number to a floating point number.
17	rational, rationalize Converts a real number to rational number.
18	numerator, denominator Returns the respective parts of a rational number.
19	realpart, imagpart Returns the real and imaginary part of a complex number.

Example

Update the source code file named main.lisp and type the following code in it.

main.lisp

; evaluate and print division result
(write (/ 45 78))
; terminate printing
(terpri)
; evaluate and print floor result
(write (floor 45 78))
; terminate printing
(terpri)
; evaluate and print division result
(write (/ 3456 75))
; terminate printing
(terpri)
; evaluate and print floor result
(write (floor 3456 75))
; terminate printing
(terpri)
; evaluate and print ceiling result
(write (ceiling 3456 75))
; terminate printing
(terpri)
; evaluate and print truncate result
(write (truncate 3456 75))
; terminate printing
(terpri)
; evaluate and print round result
(write (round 3456 75))
; terminate printing
(terpri)
; evaluate and print floor as floating result
(write (ffloor 3456 75))
; terminate printing
(terpri)
; evaluate and print ceiling as floating result
(write (fceiling 3456 75))
; terminate printing
(terpri)
; evaluate and print truncate as floating result
(write (ftruncate 3456 75))
; terminate printing
(terpri)
; evaluate and print round as floating result
(write (fround 3456 75))
; terminate printing
(terpri)
; evaluate and print mod as result
(write (mod 3456 75))
; terminate printing
(terpri)
; set c as complex number
(setq c (complex 6 7))
; print c
(write c)
; terminate printing
(terpri)
; write complex number
(write (complex 5 -9))
; terminate printing
(terpri)
; write real part of c
(write (realpart c))
; terminate printing
(terpri)
; write imaginary part of c
(write (imagpart c))

Output

When you execute the code, it returns the following result −

15/26
0
1152/25
46
47
46
46
46.0
47.0
46.0
46.0
6
#C(6 7)
#C(5 -9)
6
7

Print Page