Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to implement a gradient descent in Python to find a local minimum?
Gradient descent is a prominent optimization approach in machine learning for minimizing a model's loss function. In layman's terms, it entails repeatedly changing the model's parameters until the ideal range of values is discovered that minimizes the loss function. The method operates by making tiny steps in the direction of the loss function's negative gradient, or, more specifically, the path of steepest descent. The learning rate, a hyperparameter that regulates the algorithm's trade-off between speed and accuracy, affects the size of the steps. Many machine learning methods, including linear regression, logistic regression, and neural networks, to mention a few, employ gradient descent. Its primary application is in model training, where the goal is to minimize the difference between the target variable's anticipated and actual values. In this post, we will look at implementing a gradient descent in Python to find a local minimum.
Now it’s time to implement gradient descent in Python. Below is the basic instruction on how we will implement it −
First, we import the necessary libraries.
Defining the functions and derivative of it.
Next, we will apply the gradient descent function.
After applying the function, we will set the parameters to find the local minima,
At last, we will plot the graph of output.
Implementing Gradient Descent in Python
Importing libraries
import numpy as np import matplotlib.pyplot as plt
We then define the function f(x) and its derivative f'(x) −
def f(x): return x**2 - 4*x + 6 def df(x): return 2*x - 4
F(x) is the function that has to be decreased, and df is its derivative (x). The gradient descent approach makes use of the derivative to guide itself toward the minimum by revealing the function's slope along the way.
The gradient descent function is then defined.
def gradient_descent(initial_x, learning_rate, num_iterations):
x = initial_x
x_history = [x]
for i in range(num_iterations):
gradient = df(x)
x = x - learning_rate * gradient
x_history.append(x)
return x, x_history
The starting value of x, the learning rate, and the desired number of iterations are sent to the gradient descent function. In order to save the values of x after each iteration, it initializes x to its original value and generates an empty list. The method then executes the gradient descent for the provided number of iterations, changing x every iteration in accordance with the equation x = x - learning rate * gradient. The function produces a list of every iteration's x values together with the final value of x.
The gradient descent function may now be used to locate the local minimum of f(x) −
Example
initial_x = 0
learning_rate = 0.1
num_iterations = 50
x, x_history = gradient_descent(initial_x, learning_rate, num_iterations)
print("Local minimum: {:.2f}".format(x))
Output
Local minimum: 2.00
In this illustration, x is set to 0 at the beginning, with a learning rate of 0.1, and 50 iterations are run. Finally, we publish the value of x, which ought to be close to the local minimum at x=2.
Plotting the function f(x) and the values of x for each iteration allows us to see the gradient descent process in action −
Example
# Create a range of x values to plot
x_vals = np.linspace(-1, 5, 100)
# Plot the function f(x)
plt.plot(x_vals, f(x_vals))
# Plot the values of x at each iteration
plt.plot(x_history, f(np.array(x_history)), 'rx')
# Label the axes and add a title
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Gradient Descent')
# Show the plot
plt.show()
Output
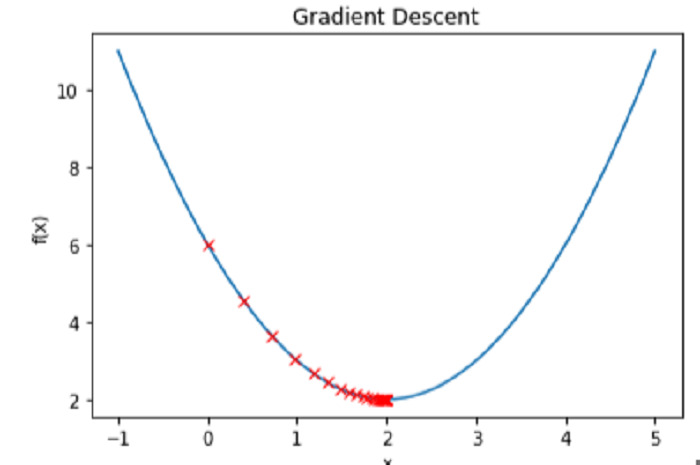
Conclusion
In conclusion, to find the local minimum of a function, Python makes use of the effective optimization process known as gradient descent. Gradient descent updates the input value repeatedly in the direction of the steepest fall until it achieves the lowest by computing the derivative of the function at each step. Implementing gradient descent in Python entails specifying the function to optimize and its derivative, initializing the input value, and determining the algorithm's learning rate and the number of iterations. When the optimization is finished, the method can be assessed by tracing its steps to the minimum and seeing how it reached it. Gradient descent can be a useful technique in machine learning and optimization applications since Python can handle big datasets and sophisticated functions.
2K+ Views
