How to generate or list all possible permutations in Excel?

Permutation can be defined as the arrangement of objects in a specific order. In this article, the user would understand the method of generating the permutation by using the VBA code. To do so, the user needs to open the code editor for VBA and after that simply click on the "OK" button. Finally, run the written code, and the permutation sequence will be displayed on the sheet normally. Refer to all the listed steps, to understand the complete method.

Example 1: To generate or list all possible permutations in excel by using the VBA code

Step 1

To understand the process of generating all the possible permutation in excel. In this example user will be able to calculate all the possible permutation combination, by using the VBA code.

Consider the below given worksheet ?

Step 2

Go to the "Developer" tab and then under the "Code" section go to the "Visual Basic" tab. Consider the below given image for proper reference ?

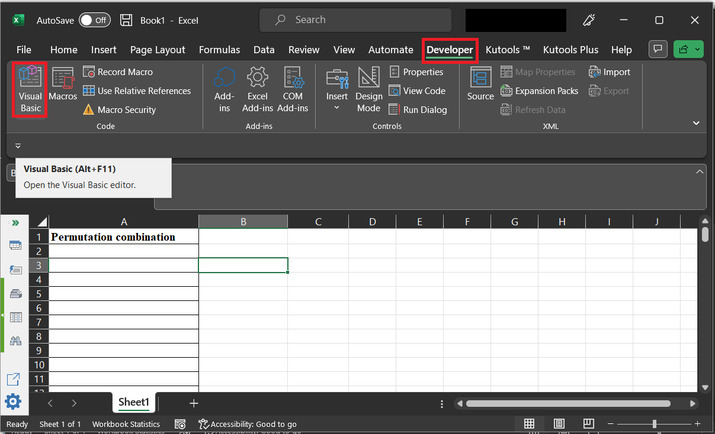
Step 3

The newly opened dialog box is of "Microsoft Visual Basic for Applications". This will open the below given code window ?

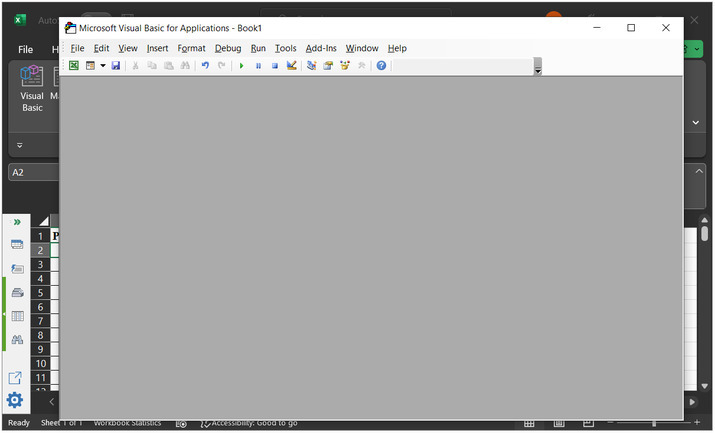
Step 4

In the dialog box, open the "Insert" option, and then click on "Module". Consider the below depicted image for reference

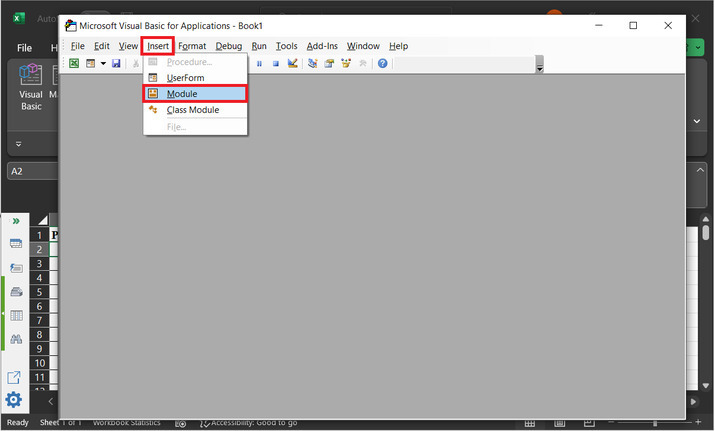
Step 5

This will open a blank code area ?

Step 6

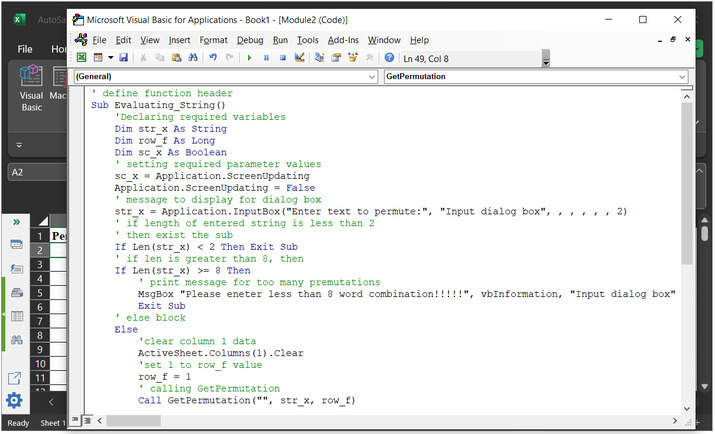
Type the below-given code to the editor ?

' define function header
Sub Evaluating_String()
   'Declaring required variables
   Dim str_x As String
   Dim row_f As Long
   Dim sc_x As Boolean
   ' setting required parameter values
   sc_x = Application.ScreenUpdating
   Application.ScreenUpdating = False
   ' message to display for dialog box
   str_x = Application.InputBox("Enter text to permute:", "Input dialog box", , , , , , 2)
   ' if length of entered string is less than 2
      ' then exist the sub
   If Len(str_x) < 2 Then Exit Sub
      ' if len is greater than 8, then
   If Len(str_x) >= 8 Then
      ' print message for too many premutations
      MsgBox "Please eneter less than 8 word combination!!!!!", vbInformation, "Input dialog box"
      Exit Sub
   ' else block
   Else
      'clear column 1 data
      ActiveSheet.Columns(1).Clear
      'set 1 to row_f value
      row_f = 1
      ' calling GetPermutation
      Call GetPermutation("", str_x, row_f)
   End If
      Application.ScreenUpdating = sc_x
End Sub
' defining submodule
Sub GetPermutation(str_1 As String, str_2 As String, ByRef row_x As Long)
   Dim i As Integer, len_x As Integer
   ' calculating the required length
   len_x = Len(str_2)
   ' if expression
   If len_x < 2 Then
      ' calculating range data
      Range("A" & row_x) = str_1 & str_2
      row_x = row_x + 1
   ' else block
   Else
      ' for each block
      For i = 1 To len_x
         ' calling permutation
         Call GetPermutation(str_1 + Mid(str_2, i, 1), Left(str_2, i - 1) + Right(str_2, len_x - i), row_x)
      Next
   End If
End Sub

A snapshot of the code area is given below ?

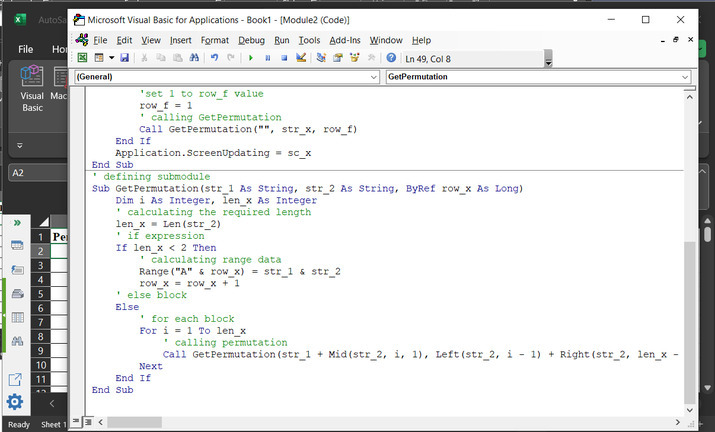
To ensure the proper execution of the result, mind the proper syntax, and code indentation.

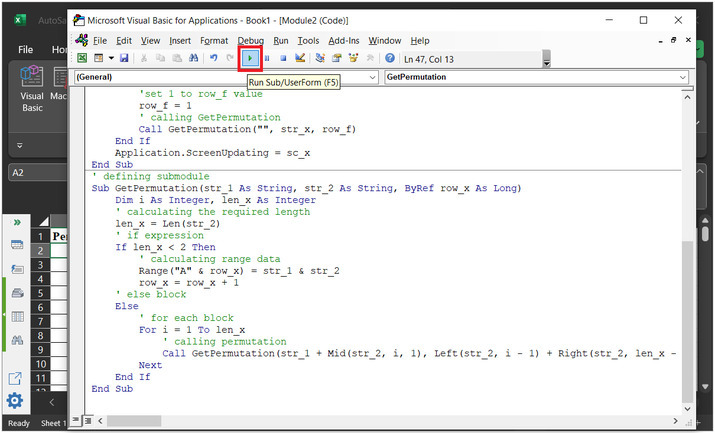
Step 7

Click on the "Run" button, shown below ?

Step 8

After that, a new dialog box, with the name "Macros" displays the above-declared module name.

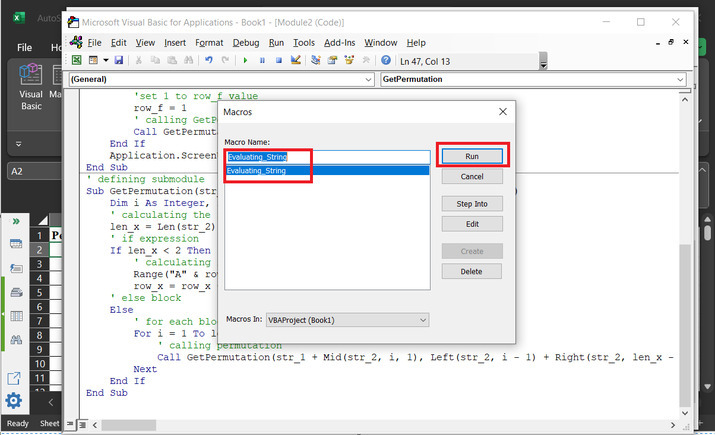
Step 9

This will open the "Input dialog box", with an input label. Users can enter the data want to create a permutation combination.

Step 10

Type data as "A2#", and click on "OK".

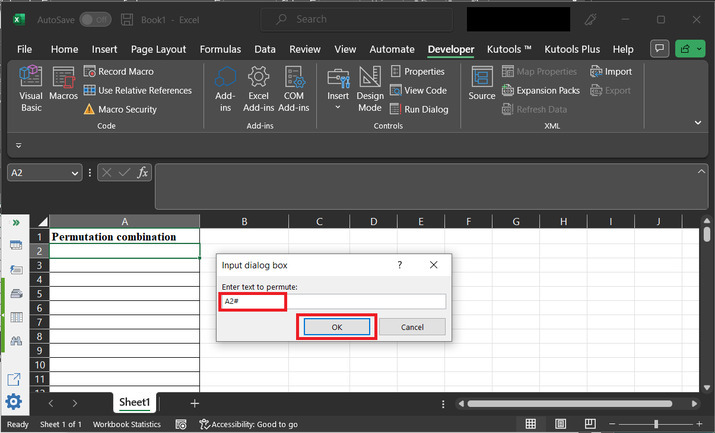
Step 11

This will display the possible permutations as given below ?

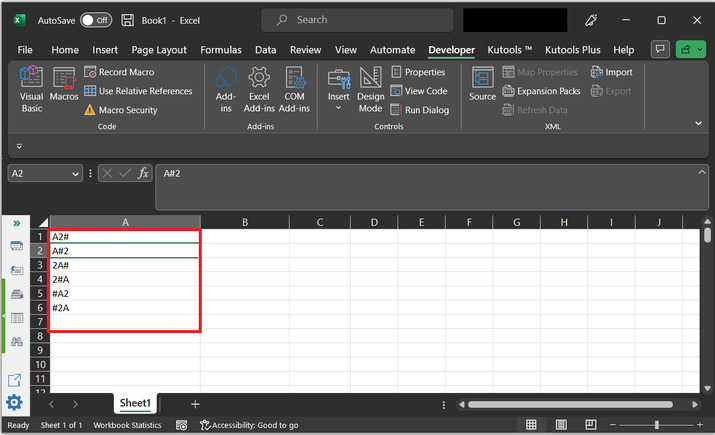
Conclusion

After completing the above article user will be able to generate the permutation sequence from the provided string data by using the VBA code. The only fact considered by using the VBA code is to use proper syntax to execute the provided code statement and to write the proper code as specified above. In this case, 3 characters are passed to the string, and the obtained number of results are $\mathrm{2^{3}\:=\:6}$.