Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Golang Program Right View of Binary Tree
In programming, there is a coding problem of binary tree that gets asked very frequently in interviews and the problem statement is to find the right view of a binary tree. If we try to understand the problem statement more than what exactly the right view is then we can explain it in a way that all the nodes are visible when you see them by standing on the right side of the tree.
Illustration
Let us understand more with the help of an example. Suppose we have a below tree and if we stand on the right side the node that is visible will be 1, 4, and 7. Nodes 3 and 2 are hidden by node 4 and node 5 and node 6 are hidden by node 7. To implement this we will do level order traversal using the Breadth First Search algorithm. For each level we will start from the right side and keep updating a variable at the end of each level the value of the variable will be the leftmost value.
Level 1: Iterate Node 1, no node on left move to next level. Node 1 is visible at this level in the right view.
Level 2: Start iterating node 2 and update the value of the variable. Move to node 3 and update the variable value and then move to node 4. Node 4 is visible at this level in the left view.
Level 3: Start with node 5 and update the value of the variable. Move to node 6 and update the variable value and then move to node 7. Node 7 is visible at this level in the left view.
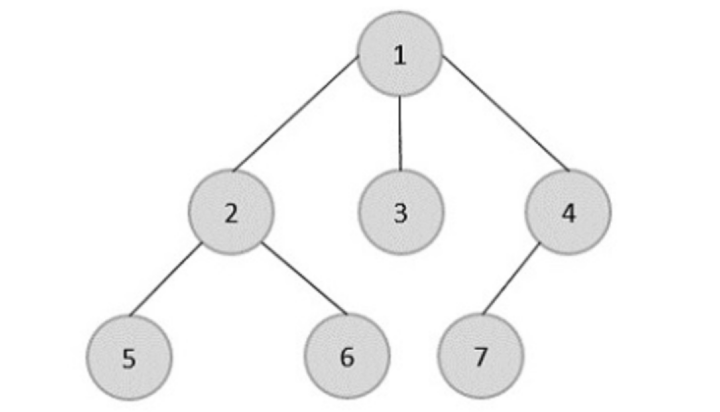
Example
In this code, we have implemented a queue data structure and its functions as well as currently there is no pre − build library for queues in Golang.
package main
import "fmt"
type Queue struct {
List [](*TreeNode)
}
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
// function to add element in queue
func (q *Queue) Enqueue(element *TreeNode) {
q.List = append(q.List, element)
}
// function to delete element in the queue
func (q *Queue) Dequeue() *TreeNode {
if q.isEmpty() {
fmt.Println("Queue is empty.")
return nil
}
element := q.List[0]
q.List = q.List[1:]
return element
}
// function check that queue is empty or not
func (q *Queue) isEmpty() bool {
return len(q.List) == 0
}
// function to find the length of the queue
func (q *Queue) size() int {
return len(q.List)
}
// creating binary tree
func CreateBinaryTree(root *TreeNode) {
n1 := TreeNode{1, nil, nil}
n2 := TreeNode{2, nil, nil}
root.Left = &n1
root.Right = &n2
n3 := TreeNode{3, nil, nil}
n4 := TreeNode{4, nil, nil}
n1.Left = &n3
n1.Right = &n4
n5 := TreeNode{5, nil, nil}
n6 := TreeNode{6, nil, nil}
n2.Left = &n5
n2.Right = &n6
}
// RightView a function with root node as argument
// and returns the right view elements in the array
func RightView(root *TreeNode) []int {
// returning empty array if tree is empty
if root == nil {
return []int{}
}
// creating vaiable for queue
var q Queue
// creating array to store right side element
var rightView []int
// variable to store right most value at current level
var Val int
// enqueue root address in the queue
q.Enqueue(root)
q.Enqueue(nil)
// breadth first search over tree
for q.size() > 1 {
currNode := q.Dequeue()
if currNode == nil {
q.Enqueue(nil)
rightView = append(rightView, Val)
continue
}
Val = currNode.Val
if currNode.Left != nil {
q.Enqueue(currNode.Left)
}
if currNode.Right != nil {
q.Enqueue(currNode.Right)
}
}
rightView = append(rightView, Val)
return rightView
}
func main() {
fmt.Println("Golang program to find right view of binary tree.")
// creating root node of binary tree
root := TreeNode{0, nil, nil}
// calling CreateBinaryTree function to create complete binary tree
CreateBinaryTree(&root)
// calling RightView function
rightView := RightView(&root)
// print right view element
for i := 0; i < len(rightView); i++ {
fmt.Print(rightView[i], " ")
}
fmt.Println()
}
Output
Golang program to find right view of binary tree. 0 2 6
Conclusion
In this way, we have found the right view of a binary tree by doing the level order traversal, using breadth first search algorithm. We can use the Depth First search algorithm also to find the level order traversal of a tree. The time complexity of this approach is O(V + E) where V and E are the no. of vertices and no. of edges in the graph. To learn more about Golang you can explore these tutorials.
71 Views
To Continue Learning Please Login