Find the largest Perfect Subtree in a given Binary Tree in Python

Suppose we have a given Binary Tree; we have to find the size of largest Perfect sub-tree in that given Binary Tree. As we know the perfect binary tree is a binary tree in which all internal nodes have two children and all leaves are at the identical level.

So, if the input is like

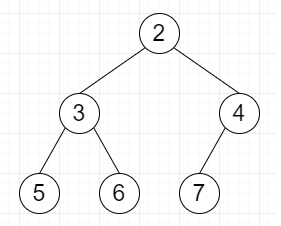
then the output will be 3, and the subtree is

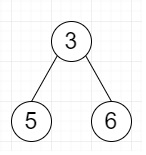
To solve this, we will follow these steps −

• Define one block called RetType, this will hold isPerfect, height and rootTree, they are all initially 0

• Define a function called get_prefect_subtree(), this takes root

• r_type := a new RetType

• if root is same as None, then

  • r_type.isPerfect := True

  • r_type.height := 0

  • r_type.rootTree := null

  • return r_type

• left_subtree := get_prefect_subtree(root.left)

• right_subtree := get_prefect_subtree(root.right)

• if left_subtree is perfect and right_subtree is perfect and height of left_subtree is same as height of right_subtree, then

  • height of r_type := height of left_subtree + 1

  • set r_type is perfect

  • r_type.rootTree := root

  • return r_type

• set r_type is not perfect

• r_type.height := maximum of height of left_subtree, height of right_subtree

• if height of left_subtree > height of right_subtree, then

  • r_type.rootTree := left_subtree.rootTree

• otherwise,

  • r_type.rootTree := right_subtree.rootTree

• return r_type

Example 

Let us see the following implementation to get better understanding −

 Live Demo

class TreeNode:
   def __init__(self, data, left = None, right = None):
      self.data = data
      self.left = left
      self.right = right
def print_tree(root):
   if root is not None:
      print_tree(root.left)
      print(root.data, end = ', ')
      print_tree(root.right)
class RetType:
   def __init__(self):
      isPerfect = 0
      height = 0
      rootTree = 0
def get_prefect_subtree(root):
   r_type = RetType()
   if (root == None) :
      r_type.isPerfect = True
      r_type.height = 0
      r_type.rootTree = None
      return r_type
   left_subtree = get_prefect_subtree(root.left)
   right_subtree = get_prefect_subtree(root.right)
   if (left_subtree.isPerfect and right_subtree.isPerfect and left_subtree.height == right_subtree.height) :
      r_type.height = left_subtree.height + 1
      r_type.isPerfect = True
      r_type.rootTree = root
      return r_type
   r_type.isPerfect = False
   r_type.height = max(left_subtree.height, right_subtree.height)
   if (left_subtree.height > right_subtree.height ):
      r_type.rootTree = left_subtree.rootTree
   else :
      r_type.rootTree = right_subtree.rootTree
   return r_type

root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.left.left = TreeNode(5)
root.left.right = TreeNode(6)
root.right.left = TreeNode(7)

res = get_prefect_subtree(root)
h = res.height

print ("Size: " , pow(2, h) - 1)
print ("Tree: ", end = " ")
print_tree(res.rootTree)

Input

root = TreeNode(2)
root.left = TreeNode(3)
root.right = TreeNode(4)
root.left.left = TreeNode(5)
root.left.right = TreeNode(6)
root.right.left = TreeNode(7)

Output

Size: 3
Tree: 5, 3, 6,