Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find n-th node in Postorder traversal of a Binary Tree in C++
In this problem, we are given a binary tree and an integer N. The task is to find the n-th node in Postorder traversal of a Binary Tree.
A binary tree has a special condition that each node can have a maximum of two children.
Traversal is a process to visit all the nodes of a tree and may print their values too.
Let’s take an example to understand the problem,
Input
N = 6
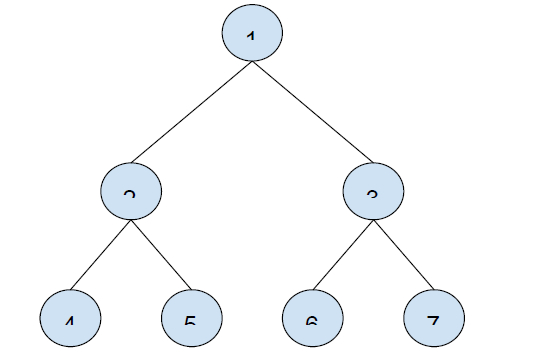
Output
3
Explanation
Post order traversal of tree − 4, 5, 2, 6, 7, 3, 1
Solution Approach
The idea is to use the post order traversal of the binary tree which is done by using recursive call. In each call we will find call postOrder() for left subtree first and then call postOrder() and at the end end visit the root node. During this traversal, we will count the number of nodes and print the node for which the count is N.
Program to illustrate the working of our solution,
Example
#include <iostream>
using namespace std;
bool isAPrimeNumber(int n) {
if (n <= 1) return false;
if (n <= 3) return true;
if (n%2 == 0 || n%3 == 0) return false;
for (int i=5; i*i<=n; i=i+6)
if (n%i == 0 || n%(i+2) == 0)
return false;
return true;
}
long int calcPrimeProduct(long int n) {
long int p = 2;
n--;
for (int i = 3; n != 0; i++) {
if (isAPrimeNumber(i)) {
p = p * i;
n--;
}
i++;
}
return p;
}
long int findNextPrime(long int n) {
long int nextPrime = n + 2;
while (true) {
if (isAPrimeNumber(nextPrime))
break;
nextPrime++;
}
return nextPrime;
}
int main() {
long long int N = 5;
long long int primeProduct = calcPrimeProduct(N);
int fortunateNumber = findNextPrime(primeProduct) - primeProduct;
cout<<N<<"th fortunate number is "<<fortunateNumber;
return 0;
}Output
5th fortunate number is 23
75 Views
