Article Categories
- All Categories
-
 Data Structure
Data Structure
-
 Networking
Networking
-
 RDBMS
RDBMS
-
 Operating System
Operating System
-
 Java
Java
-
 MS Excel
MS Excel
-
 iOS
iOS
-
 HTML
HTML
-
 CSS
CSS
-
 Android
Android
-
 Python
Python
-
 C Programming
C Programming
-
 C++
C++
-
 C#
C#
-
 MongoDB
MongoDB
-
 MySQL
MySQL
-
 Javascript
Javascript
-
 PHP
PHP
Postorder traversal of Binary Tree without recursion and without stack in C++
In this problem, we are given a Binary tree. Our task is to print the postorder traversal of the binary tree without using recursion and without stack.
Binary tree is a special type of tree in which each node can have at max 2 child nodes.
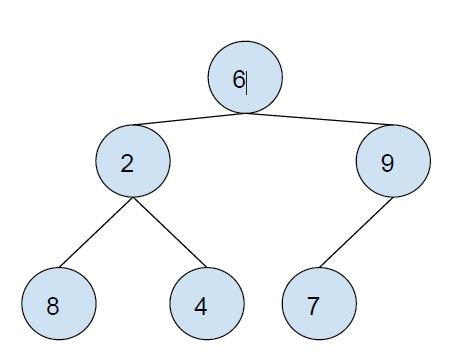
Postorder Traversal is a tree traversal technique, in which the first left subtree is traversed than the right subtree and the root is traversed at the end.
postorder traversal of the above tree − 8 4 2 7 9 6
To traverse the tree without using recursion and stack. We will depth-first search based technique and data will be stored in a hash table.
Example
Program to show the implementation of this solution,
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
};
void postOrderTraversal(struct Node* head) {
struct Node* temp = head;
unordered_set<Node*> visited;
while (temp && visited.find(temp) == visited.end()) {
if (temp->left &&
visited.find(temp->left) == visited.end())
temp = temp->left;
else if (temp->right &&
visited.find(temp->right) == visited.end())
temp = temp->right;
else {
cout<<temp->data<<"\t";
visited.insert(temp);
temp = head;
}
}
}
struct Node* insertNode(int data){
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
return (node);
}
int main(){
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
}
Output
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6
The same solution can be updated and the usage of the hash table can be eliminated. As its work is to store visited nodes. We will add a visited flag to every node it the tree itself to reduce the load on the system, this will make our algorithm better.
A more effective solution is using an unordered map, this will reduce the overhead of trackback to the head.
Example
Program to show the implementation
#include <bits/stdc++.h>
using namespace std;
struct Node {
int data;
struct Node *left, *right;
bool visited;
};
void postOrderTraversal(Node* root) {
Node* n = root;
unordered_map<Node*, Node*> postorder;
postorder.insert(pair<Node*, Node*>(root, nullptr));
while (n) {
if (n->left && postorder.find(n->left) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->left, n));
n = n->left;
}
else if (n->right && postorder.find(n->right) == postorder.end()) {
postorder.insert(pair<Node*, Node*>(n->right, n));
n = n->right;
}
else {
cout<<n->data<<"\t";
n = (postorder.find(n))->second;
}
}
}
struct Node* insertNode(int data) {
struct Node* node = new Node;
node->data = data;
node->left = NULL;
node->right = NULL;
node->visited = false;
return (node);
}
int main() {
struct Node* root = insertNode(6);
root->left = insertNode(2);
root->right = insertNode(9);
root->left->left = insertNode(8);
root->left->right = insertNode(4);
root->right->left = insertNode(7);
root->right->left->left = insertNode(13);
cout<<"Post Order Traversal of the binary tree :\n";
postOrderTraversal(root);
return 0;
}
Output
Post Order Traversal of the binary tree : 8 4 2 13 7 9 6


