Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find LCA in Binary Tree using RMQ in C++
Concept
The article explains a method to solving the problem of finding the LCA of two nodes in a tree by reducing it to a RMQ problem.
Examples
Lowest Common Ancestor (LCA) of two nodes a and b in a rooted tree T is defined as the node located farthest from the root that has both a and b as descendants.
For example, according to below diagram, LCA of node D and node I is node B.
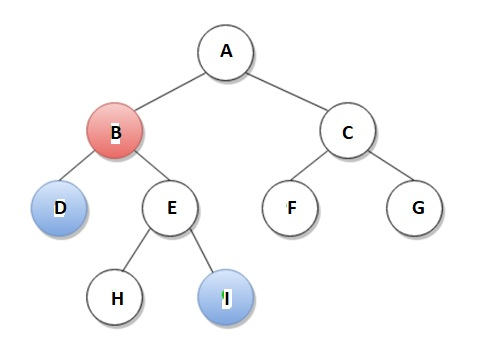
We can apply so many approaches to solve the LCA problem. These approaches differ with respect of their time and space complexities.
Range Minimum Query (RMQ) is applied on arrays to locate the position of an element with the minimum value between two specified indices. We can apply different approaches for solving RMQ. According to this article, Segment Tree based approach is explained. With respect of segment tree, preprocessing time is O(n) and time to for range minimum query is O(Logn). Here, the extra space needed is O(n) to store the segment tree.
Reduction of LCA to RMQ
We explain this idea to visit the tree starting from root by an Euler tour (Visit without lifting pencil), which is a DFS(Depth First Search)-type traversal with preorder traversal characteristics.
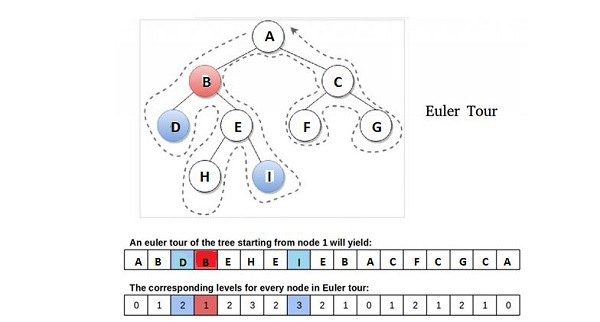
Observation − According to above diagram, the LCA of nodes D and I is node B, which indicates to be the node closest to the root amongst all those encountered between the visits of D and I during a DFS of T. So we can say this observation is the key to the reduction. Again we can say that our node is the node at the minimum level and the only node at that level amongst all the nodes that occur between consecutive occurrences (any) of a and b in the Euler tour of T.
We require three arrays for implementation −
Visited nodes in order of Euler tour of T
Each node Level visited in Euler tour of T
Node’s first occurrence index in Euler tour of T (since any occurrence would be good, let’s track the first one)
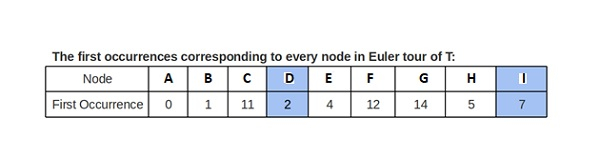
Method
Perform a Euler tour on the tree, and fill the euler, level and first occurrence arrays.
Applying the first occurrence array, obtain the indices corresponding to the two nodes which will be the corners of the range in the level array that is fed to the RMQ algorithm for the minimum value.
At the time when the algorithm returns the index of the minimum level in the range, we apply it to determine the LCA using Euler tour array.
Example
/* This C++ Program is implemented to find LCA of u and v by reducing the problem to RMQ */
#include<bits/stdc++.h>
#define V 9 // indicates number of nodes in input tree
int euler1[2*V - 1]; // indicates for Euler tour sequence
int level1[2*V - 1]; // indicates level of nodes in tour sequence
int firstOccurrence1[V+1]; // indicates first occurrences of nodes in tour
int ind; // indicates variable to fill-in euler and level arrays
//This is a Binary Tree node
struct Node1{
int key;
struct Node1 *left, *right;
};
// Utility function creates a new binary tree node with given key
Node1 * newNode1(int k){
Node1 *temp = new Node1;
temp->key = k;
temp->left = temp->right = NULL;
return temp;
}
// indicates log base 2 of x
int Log2(int x){
int ans = 0 ;
while (x>>=1) ans++;
return ans ;
}
/* A recursive function is used to get the minimum value in a given range of array indexes. The following are parameters for this function.
st --> indicates pointer to segment tree
index --> indicates index of current node in the segment tree.
Initially 0 is passed as root is always at index 0
ss & se --> indicate starting and ending indexes of the segment
represented by current node, i.e., st[index]
qs & qe --> indicate starting and ending indexes of query range
*/
int RMQUtil(int index1, int ss1, int se1, int qs1, int qe1, int *st1){
// It has been seen that if segment of this node is a part of given range, then return the min of the segment
if (qs1 <= ss1 && qe1 >= se1)
return st1[index1];
//It has been seen that if segment of this node is outside the given range
else if (se1 < qs1 || ss1 > qe1)
return -1;
// It has been seen that if a part of this segment overlaps with the given range
int mid = (ss1 + se1)/2;
int q1 = RMQUtil(2*index1+1, ss1, mid, qs1, qe1, st1);
int q2 = RMQUtil(2*index1+2, mid+1, se1, qs1, qe1, st1);
if (q1==-1) return q2;
else if (q2==-1) return q1;
return (level1[q1] < level1[q2]) ? q1 : q2;
}
// Return minimum of elements in range from index qs (query start) to
// qe (query end). It mainly uses RMQUtil()
int RMQ(int *st1, int n, int qs1, int qe1){
// Check for erroneous input values
if (qs1 < 0 || qe1 > n-1 || qs1 > qe1){
printf("Invalid Input");
return -1;
}
return RMQUtil(0, 0, n-1, qs1, qe1, st1);
}
// Now a recursive function that constructs Segment Tree for
array[ss1..se1]. // si1 is index of current node in segment tree st
void constructSTUtil(int si1, int ss1, int se1, int arr1[], int *st1){
// When there will be only one element in array, store it in current node of
// segment tree and return
if (ss1 == se1)st1[si1] = ss1;
else{
// It has been seen that if there are more than one
elements, then recur for left and right subtrees and store the
minimum of two values in this node
int mid1 = (ss1 + se1)/2;
constructSTUtil(si1*2+1, ss1, mid1, arr1, st1);
constructSTUtil(si1*2+2, mid1+1, se1, arr1, st1);
if (arr1[st1[2*si1+1]] < arr1[st1[2*si1+2]])
st1[si1] = st1[2*si1+1];
else
st1[si1] = st1[2*si1+2];
}
}
/* Now this function is used to construct segment tree from given
array. This function allocates memory for segment tree and calls
constructSTUtil() to fill the allocated memory */
int *constructST(int arr1[], int n){
// Allocating memory for segment tree
//Indicates height of segment tree
int x = Log2(n)+1;
// Indicates maximum size of segment tree
int max_size = 2*(1<<x) - 1; // 2*pow(2,x) -1
int *st1 = new int[max_size];
// Indicates filling the allocated memory st1
constructSTUtil(0, 0, n-1, arr1, st1);
// Returning the constructed segment tree
return st1;
}
// Indicates recursive version of the Euler tour of T
void eulerTour(Node1 *root, int l){
/* if the passed node exists */
if (root){
euler1[ind] = root->key; // inserting in euler array
level1[ind] = l; // inserting l in level array
ind++; // indicates increment index
/* It has been seen that if unvisited, mark first occurrence*/
if (firstOccurrence1[root->key] == -1)
firstOccurrence1[root->key] = ind-1;
/* touring left subtree if exists, and remark euler
and level arrays for parent on return */
if (root->left){
eulerTour(root->left, l+1);
euler1[ind]=root->key;
level1[ind] = l;
ind++;
}
/* touring right subtree if exists, and remark euler
and level arrays for parent on return */
if (root->right) {
eulerTour(root->right, l+1);
euler1[ind]=root->key;
level1[ind] = l;
ind++;
}
}
}
// Returning LCA of nodes n1, n2 (assuming they are
// present in the tree)
int findLCA(Node1 *root, int u1, int v1){
/* Marking all nodes unvisited. Note that the size of
firstOccurrence is 1 as node values which vary from
1 to 9 are used as indexes */
memset(firstOccurrence1, -1, sizeof(int)*(V+1));
/* To start filling euler and level arrays from index 0 */
ind = 0;
/* Starting Euler tour with root node on level 0 */
eulerTour(root, 0);
/* constructing segment tree on level array */
int *st1 = constructST(level1, 2*V-1);
/*It has been seen that if v before u in Euler tour. For RMQ to
work, first parameter 'u1' must be smaller than second 'v1' */
if (firstOccurrence1[u1]>firstOccurrence1[v1])
std::swap(u1, v1);
// Indicates starting and ending indexes of query range
int qs1 = firstOccurrence1[u1];
int qe1 = firstOccurrence1[v1];
// Indicates query for index of LCA in tour
int index1 = RMQ(st1, 2*V-1, qs1, qe1);
/* returning LCA node */
return euler1[index1];
}
// Driver program to test above functions
int main(){
// Let us create the Binary Tree as shown in the diagram.
Node1 * root = newNode1(1);
root->left = newNode1(2);
root->right = newNode1(3);
root->left->left = newNode1(4);
root->left->right = newNode1(5);
root->right->left = newNode1(6);
root->right->right = newNode1(7);
root->left->right->left = newNode1(8);
root->left->right->right = newNode1(9);
int u1 = 4, v1 = 9;
printf("The LCA of node %d and node %d is node %d.\n",
u1, v1, findLCA(root, u1, v1));
return 0;
}Output
The LCA of node 4 and node 9 is node 2.
89 Views
