Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Fibonacci Heaps in Data Structure
Like Binomial heaps, Fibonacci heaps are collection of trees. They are loosely based on binomial heaps. Unlike trees with in binomial heaps are ordered trees within Fibonacci heaps are rooted but unordered.
Each node x in Fibonacci heaps contains a pointer p[x] to its parent, and a pointer child[x] to any one of its children. The children of x are linked together in a circular doubly linked list known as child list of x. Each child y in a child list has pointers left[y] and right[y] to point left and right siblings of y respectively. If node y is only child then left[y] = right[y] = y. The order in which sibling appears in a child list is arbitrary.
Example of Fibonacci Heap
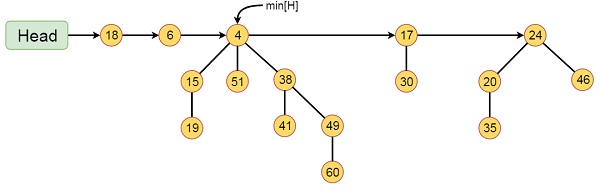
This Fibonacci Heap H consists of five Fibonacci Heaps and 16 nodes. The line with arrow head indicates the root list. Minimum node in the list is denoted by min[H] which is holding 4.
The asymptotically fast algorithms for problems such as computing minimum spanning trees, finding single source of shortest paths etc. makes essential use of Fibonacci heaps.
887 Views
