Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binomial Heaps in Data Structure
A binomial Heap is a collection of Binomial Trees. A binomial tree Bk is an ordered tree defined recursively. A binomial Tree B0 is consists of a single node.
A binomial tree Bk is consisting of two binomial tree Bk-1. That are linked together. The root of one is the left most child of the root of the other
Some binomial heaps are like below −
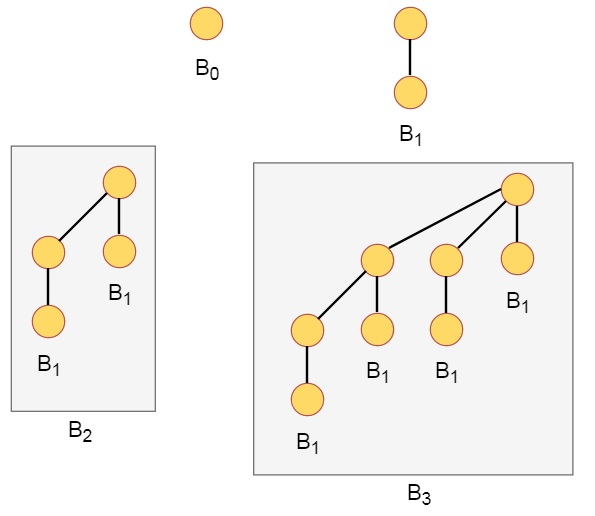
Some properties of binomial trees are −
Binomial tree with Bk has 2k nodes.
Height of the tree is k
There are exactly $$\left(\begin{array}{c}k\ j\end{array}\right)$$ nodes at depth i for all i in range 0 to k
Binomial Heap
A binomial heap H is a set of binomial trees. There are some properties.
Each binomial tree in H is heap-ordered. So the key of a node is greater than or equal to the key of its parent.
There is at most one binomial tree in H, whose root has a given degree.
Example of Binomial Heap
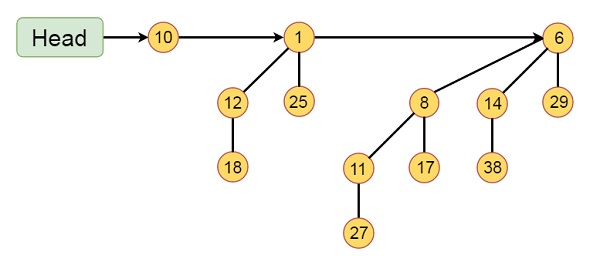
This binomial Heap H consists of binomial trees B0, B2 and B3. Which have 1, 4 and 8 nodes respectively. And in total n = 13 nodes. The root of binomial trees are linked by a linked list in order of increasing degree
2K+ Views
