Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Faraday’s Laws and Lenz’s Law of Electromagnetic Induction
Faraday’s Laws of Electromagnetic Induction
Michael Faraday (an English scientist) performed a series of experiments to demonstrate the phenomenon of electromagnetic induction and he summed up his conclusions into two laws, known as Faraday's laws of electromagnetic induction.
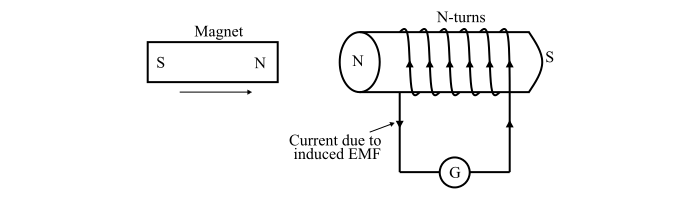
First Law of Electromagnetic Induction
The first law states that "when a magnetic flux linking a conductor or coil changes, an EMF is induced in the conductor or coil". Therefore, the first law tells about the condition under which the emf is induced in a conductor or coil.
Second Law of Electromagnetic Induction
The second law states that "The magnitude of the induced emf in the conductor or coil is directly proportional to the rate of change of magnetic flux linkages". Therefore, the second law gives the magnitude of induced emf in the conductor or coil.
Explanation − Consider a coil has N turns and the magnetic flux linking the coil changes from $\varphi_{1}$ to $\varphi_{2}$ in t seconds. Therefore,
$$\mathrm{Initial\: magnetic\: flux \:linkage,ψ_{1} = N\varphi_{1}}$$
$$\mathrm{Final \:magnetic\: flux \:linkage, ψ_{2} = N\varphi_{2}}$$
$$\mathrm{\therefore Induced \:EMF,e\propto\frac{ψ_2-ψ_1}{t}\propto\frac{N\varphi_2-N\varphi_1}{t}}$$
$$\mathrm{\Longrightarrow e=k(\frac{N\varphi_2-N\varphi_1}{t})}$$
Where k is a constant of proportionality and in SI units its value being 1. Therefore,
$$\mathrm{\Longrightarrow e=(\frac{N\varphi_2-N\varphi_1}{t})}$$
In differential form,
$$\mathrm{e=N\frac{d\varphi}{dt}}$$
The above equation represents Faraday’s second law mathematically.
Lenz’s Law
A German scientist, Emil Lenz, gave a rule to determine the direction of induced EMF by the electromagnetic induction in a conductor or coil, which is stated as follows −
"The current due to induced emf will flow in such a direction so as to oppose the cause that produces it i.e. the current due to induced emf will set up a magnetic flux to oppose the change in magnetic flux which produced it".
Mathematically, the Lenz’s law is given by adding a minus in the R.H.S. of Faraday’s second law i.e.
$$\mathrm{e=-N\frac{d\varphi}{dt}}$$
Here, the minus sing shows that the induced emf opposes the changing magnetic field that induces it. Therefore, the Lenz’s law directly follows from the law of conservation of energy i.e. in order to induce emf in a coil or conductor, some energy must be expanded in the opposition.
Numerical Example
A magnetic flux of 25 mWb is linked with coil of 600 turns. If this magnetic flux reversed in a time of 3 ms, calculate the induced emf in the coil.
Solution
$$\mathrm{Change\: in \:magnetic\: flux,d\varphi=\varphi_{2} - \varphi_{1}=25-(-25)=50nmb}$$
$$\mathrm{Time\: taken\: for\: the\: change,dt=3ms}$$
$$\mathrm{\therefore Induced\: EMF,e = N\frac{d\varphi}{dt}=600\times(\frac{50\times10^{-3}{3}}\times10^{-3})=10000=10kV}$$
436 Views
