Document Retrieval using Boolean Model and Vector Space Model

Introduction

Document Retrieval in Machine Learning is part of a larger aspect known as Information Retrieval, where a given query by the user, the system tries to find relevant documents to the search query as well as rank them in order of relevance or match.

They are different ways of Document retrieval, two popular ones are −

• Boolean Model

• Vector Space Model

Let us have a brief understanding of each of the above methods.

Boolean Model

It is a set-based retrieval model.The user query is in boolean form. Queries are joined using AND, OR, NOT, etc. A document can be visualized as a keyword set. Based on the query a document is retrieved based on relevance. Partial matches and ranking are not supported.

Example (Boolean query) −

[[America & France] | [Honduras & London]] & restaurants &! Manhattan]

Steps and Flow diagram of Boolean Model

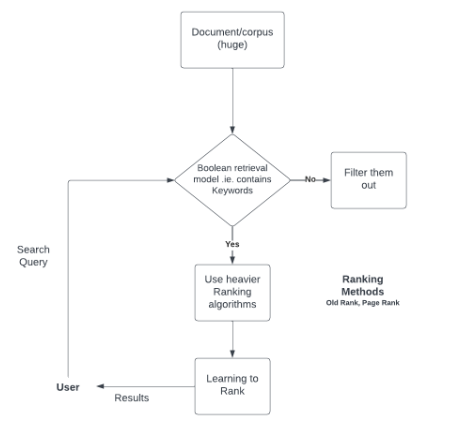
Boolean model is an Inverted Index search to find if a document is relevant or not.It does not return the rank of the document.

Let us consider we have 3 documents in our corpus.

document_id	document_text
1.	Taj Mahal is a beautiful monument
2.	Victoria Memorial is also a monument
3.	I like to visit Agra

The term matrix will be created as below.

term	doc_1	doc_2	doc_3
taj	1	0	0
mahal	1	0	0
is	1	1	0
a	1	1	0
beautiful	1	0	0
monument	1	1	0
victoria	0	1	0
memorial	0	1	0
also	0	1	0
i	0	0	1
like	0	0	1
to	0	0	1
visit	0	0	1
agra	0	0	1

let us have a query like "taj mahal agra"

The query will be created as −

taj [100] & mahal [100] & agra [001]

or 100 & 100 & 001 = 000, so here we can see none of the documents are relevant using AND.

We can then try including other operators like OR or using different keywords in addition to these.

The inverted index can be created for this corpus as −

taj - set(1)

mahal – set(1)

is - set(1,2)

a - set(1,2)

beautiful - set(1)

monument - set(1,2)

victoria – set(2)

memorial - set(2)

also - set(2)

i - set(3)

like - set(3)

to - set(3)

visit - set(3)

agra- set(3)

Vector Space Model

The vector space model is a kind f statistical model of retrieval.

• In this model, the documents are represented as a bag of words.

• The bag allows words to occur more than once

• User can use weights with search query like q = < ecommerce 0.5; products 0.8; price 0.2

• It is based on the similarity between the query and documents.

• Output is ranked documents.

• It can also encompass the multiple occurrences of words.

Graphical Representation

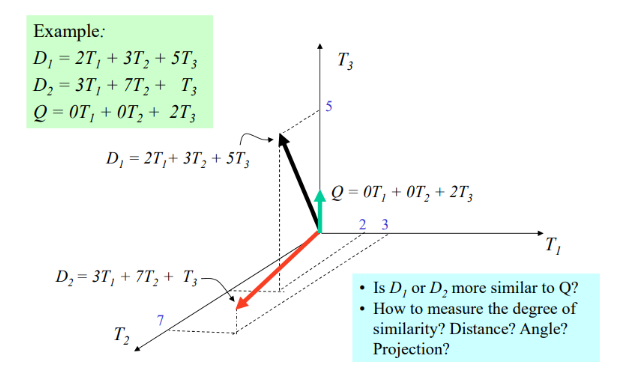
Example

import pandas as pd
from contextlib import redirect_stdout
import math
trms = []
Keys = []
vector_dic = {}
dictionary_i = {}
random_list = []
t_frequency = {}
inv_doc_freq = {}
wt = {}
def documents_filter(docs, rw, cl):
   for i in range(rw):
      for j in range(cl):
         if(j == 0):
            Keys.append(docs.loc[i].iat[j])
         else:
         
            random_list.append(docs.loc[i].iat[j])
            
            if docs.loc[i].iat[j] not in trms:
            
                     trms.append(docs.loc[i].iat[j])
                     
      listcopy = random_list.copy()
      dictionary_i.update({docs.loc[i].iat[0]: listcopy})
      random_list.clear()
      
def calc_weight(doccount, cls):
   for i in trms:
      if i not in t_frequency:
            t_frequency.update({i: 0})
            
      for key, val in dictionary_i.items():
         for k in val:
            if k in t_frequency:
               t_frequency[k] += 1
      inv_doc_freq = t_frequency.copy()
      for i in t_frequency:
         t_frequency[i] = t_frequency[i]/cls
      for i in inv_doc_freq:
         if inv_doc_freq[i] != doccount:
            inv_doc_freq[i] = math.log2(cls / inv_doc_freq[i])
         else:
         
            nv_doc_freq[i] = 0
      for i in inv_doc_freq:
         wt.update({i: inv_doc_freq[i]*t_frequency[i]})
         
      for i in dictionary_i:
         for j in dictionary_i[i]:
            random_list.append(wt[j])
            
      copy = random_list.copy()
      vector_dic.update({i: copy})
      random_list.clear()
      
def retrieve_wt_query(q):
   qFrequency = {}
   for i in trms:
      if i not in qFrequency:
         qFrequency.update({i: 0})
   for val in q:
      if val in qFrequency:
         qFrequency[val] += 1
   for i in qFrequency:
      qFrequency[i] = qFrequency[i] / len(q)
      
   return qFrequency
   
def compute_sim(query_Weight):
      num = 0
      deno1 = 0
      deno2 = 0
      sim= {}
      for doc in dictionary_i:
         for trms in dictionary_i[doc]:
            num += wt[trms] * query_Weight[trms]
            deno1 += wt[trms] * wt[trms]
            deno2 += query_Weight[trms] * query_Weight[trms]
         if deno1 != 0 and deno2 != 0:
            simi = num / (math.sqrt(deno1) * math.sqrt(deno2))
            sim.update({doc: simi})
            num = 0
            deno1 = 0
            deno2 = 0
            
      return (sim)
      
def pred(simi, doccount):

   with open('result.txt', 'w') as f:
      with redirect_stdout(f):
         ans = max(simi, key=simi.get)
         print(ans, "- most relevent document")
         print("documents rank")
         for i in range(doccount):
            ans = max(simi, key=lambda x: simi[x])
            print(ans, "ranking ", i+1)
            simi.pop(ans)
            
def main():
   docs = pd.read_csv(r'corpus_docs.csv')
   rw = len(docs)
   cls = len(docs.columns)
   documents_filter(docs, rw, cls)
   calc_weight(rw, cls)
   print("Input your query")
   q = input()
   q = q.split(' ')
   q_wt = retrieve_wt_query(q)
   sim = compute_sim(q_wt)
   pred(sim, rw)
main()

Output

Input your query
hockey
{'doc2': 0.4082482904638631}
doc2 - most relevent document
documents rank
doc2 ranking 1

Conclusion

Document retrieval is the backbone of every search task nowadays. Whether it's search, database retrieval, or general information retrieval, everywhere we find applications of models like Boolean and Vector space.