Cubic Spline Data Interpolation in MATLAB

In mathematics, the cubic spline data interpolation is a way of calculating values between data points of a given data set. This technique is widely used when we want to plot a smooth curve passing through these data points.

In MATLAB, we can calculate the cubic spline data interpolation by using any of two built-in functions namely, 'spline' or 'interp1'.

Syntax

Where, the syntax of the 'spline' function is,

I = spline(x, y, query);

Here, 'x and 'y' are the vectors containing input data points required for interpolation, and 'query' is the vector that contains data points at which we want to perform interpolation.

The syntax of the 'interp1' function is,

I = interp1(x, y, query, 'spline');

In the 'interp1' function, we use the 'spline' option to specify the operation to be performed on the input data.

How to Perform Cubic Spline Data Interpolation Using MATLAB?

The step-by-step process for performing cubic spline data interpolation on a given set of data points is explained here.

• Step (1) − Define the data points on which interpolation is to be performed.

• Step (2) − Specify the query containing the data points at which we want to perform cubic spline interpolation.

• Step (3 − Calculate the cubic spline data interpolation for the provided input data points.

• Step (4) − Display interpolation result.

• Step (5) − Plot the results of the cubic spline data interpolation.

Let us now understand practically how to compute the cubic spline data interpolation using MATLAB.

The following MATLAB programs demonstrate the computation of cubic spline interpolation of a set of given data points.

(1). Cubic Spline Interpolation Using 'spline' Function

The following MATLAB program shows how to use the 'spline' function to calculate the cubic spline interpolation of the given data.

MATLAB Program (1)

% MATLAB program to calculate cubic spline data interpolation using 'spline' function
% Define sample data points
x = 0:15;
y = cos(x);

% Specify the query containing the data points to perform interpolation
query = [2, 5, 7, 9];

% Calculate the cubic spline interpolation
I = spline(x, y, query);

% Display the results of interpolation
disp('Query Points   Interpolation Results');
disp([query' I']);

% Plot curves for original data and interpolated results
figure;
plot(x, y, '-', query, I, 'x', query, I, 'o');
title('Cubic Spline Interpolation in MATLAB');

Output

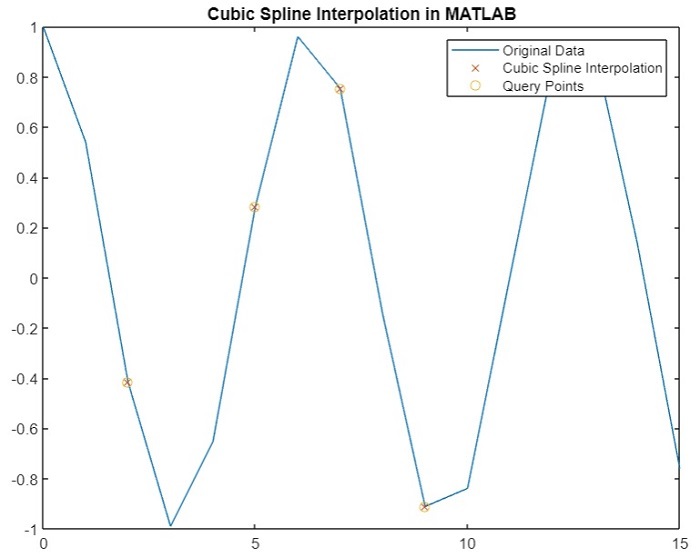
Query Points   Interpolation Results
    2.0000   -0.4161
    5.0000    0.2837
    7.0000    0.7539
    9.0000   -0.9111

You will get the following plot −

(2). Cubic Spline Interpolation Using 'interp1' Function

As we mentioned above, we can also calculate the cubic spline interpolation of a given data set using the 'interp1' function. The following MATLAB program illustrates the code implementation to calculate the cubic spline interpolation using the 'interp1' function.

Matlab Example (2)

% MATLAB program to calculate cubic spline data interpolation using 'interp1' function
% Define sample data points
x = 0:15;
y = sin(x);

% Specify the query containing the data points to perform interpolation
query = [2, 4, 8, 10];

% Calculate the cubic spline interpolation
I = interp1(x, y, query, 'spline');

% Display the results of interpolation
disp('Query Points   Interpolation Results');
disp([query' I']);

% Plot curves for original data and interpolated results
figure;
plot(x, y, '-', query, I, 'x', query, I, 'o');
legend('Original Data', 'Cubic Spline Interpolation', 'Query Points');
title('Cubic Spline Interpolation in MATLAB');

Output

Query Points   Interpolation Results
    2.0000    0.9093
    4.0000   -0.7568
    8.0000    0.9894
   10.0000   -0.5440

You will get the following plot −

Conclusion

This is all about cubic spline data interpolation calculation using MATLAB. In this tutorial, we have described the cubic spline data interpolation and the steps to calculate it using MATLAB. Also, we have demonstrated the calculation of cubic spline data interpolation using MATLAB with the help of example MATLAB programs for the better understanding.