Lagrange Interpolation

For constructing new data points within a range of a discrete set of given data point, the interpolation technique is used. Lagrange interpolation technique is one of them. When the given data points are not evenly distributed, we can use this interpolation method to find the solution. For the Lagrange interpolation, we have to follow this equation.

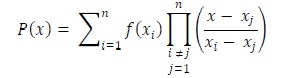
Input and Output

Input:
List of x and f(x) values. find f(3.25)
x: {0,1,2,3,4,5,6}
f(x): {0,1,8,27,64,125,216}
Output:
Result after Lagrange interpolation f(3.25) = 34.3281

Algorithm

largrangeInterpolation(x: array, fx: array, x1)

Input − x array and fx array for getting previously known data, and point x1.

Output: The value of f(x1).

Begin
   res := 0 and tempSum := 0
   for i := 1 to n, do
      tempProd := 1
      for j := 1 to n, do
         if i ≠ j, then
            tempProf := tempProd * (x1 – x[j])/(x[i] – x[j])
      done

      tempPord := tempProd * fx[i]
      res := res + tempProd
   done
   return res
End

Example

#include<iostream>
#define N 6
using namespace std;

double lagrange(double x[], double fx[], double x1) {
   double res = 0, tempSum = 0;

   for(int i = 1; i<=N; i++) {
      double tempProd = 1;         //for each iteration initialize temp product
      for(int j = 1; j<=N; j++) {
         if(i != j) {                 //if i = j, then denominator will be 0
            tempProd *= (x1 - x[j])/(x[i] - x[j]);     //multiply each term using formula
         }
      }
      tempProd *= fx[i];                //multiply f(xi)
      res += tempProd;
   }
   return res;
}

main() {
   double x[N+1] = {0,1,2,3,4,5,6};
   double y[N+1] = {0,1,8,27,64,125,216};
   double x1 = 3.25;
   cout << "Result after lagrange interpolation f("<<x1<<") = " << lagrange(x, y, x1);
}

Output

Result after lagrange interpolation f(3.25) = 34.3281

Ankith Reddy

Updated on: 17-Jun-2020

888 Views

Kickstart Your Career

Get certified by completing the course

Get Started