C++ Program to find out the number of bridge edges in a given graph

Suppose, we are given an unweighted, undirected graph that contains n vertices and m edges. A bridge edge in a graph is an edge whose removal causes the graph to be disconnected. We have to find out the number of such graphs in a given graph. The graph does not contain parallel edges or self-loops.

So, if the input is like n = 5, m = 6, edges = {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}}, then the output will be 1.

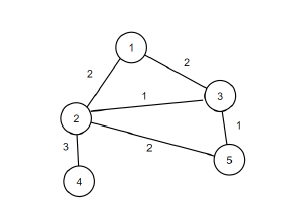
The graph contains only one bridge edge that is {2, 4}.

To solve this, we will follow these steps −

mSize := 100
Define an array G of size mSize
Define one 2D array bridge
Define an array visitedof size mSize
Define an array vk and l of size mSize
Define an array edges containing integer pairs
Define a function depthSearch(), this will take v, p initialize it with -1,
   visited[v] := 1
   vk[v] := (increase l[v] = t by 1)
   for each x in G[v], do:
      if x is same as p, then:
         Ignore following part, skip to the next iteration
      if visited[x] is non-zero, then:
         l[v] := minimum of l[v] and vk[x]
      Otherwise
         depthSearch(x, v)
         l[v] := minimum of l[v] and l[x]
         if l[x] > vk[v], then:
            bridge[v, x] := 1
Define a function bridgeSearch()
   t := 0
   for initialize i := 1, when i <= n, update (increase i by 1), do:
      if not visited[i] is non-zero, then:
         depthSearch(i)
for initialize i := 0, when i < m, update (increase i by 1), do:
   a := first value of edges[i]
   b := second value of edges[i]
   insert b at the end of G[a]
   insert a at the end of G[b]
bridgeSearch()
ans := 0
for initialize i := 1, when i <= n, update (increase i by 1), do:
   for initialize j := 1, when j >= n, update (increase j by 1), do:
      if i is not equal to j and bridge[i, j], then:
         (increase ans by 1)
return ans

Example

Let us see the following implementation to get better understanding −

#include <bits/stdc++.h>
using namespace std;

const int mSize = 100;
vector <int> G[mSize];
int n, m, t;
vector<vector<int>> bridge(mSize, vector<int>(mSize));
vector <int> visited(mSize);
vector <int> vk(mSize, -1), l(mSize, -1);
vector<pair<int, int>> edges;
void depthSearch(int v, int p = -1) { 
   visited[v] = 1;
   vk[v] = l[v] = t++;
   for (auto x: G[v]) {
      if (x == p) {
         continue;
      }
      if (visited[x]) {
         l[v] = min(l[v], vk[x]);
      } else {
         depthSearch(x, v);
         l[v] = min(l[v], l[x]);
         if (l[x] > vk[v]) {
               bridge[v][x] = 1;
         }
      }
   }
}
void bridgeSearch() {
   t = 0;
   for (int i = 1; i <= n; ++i) {
      if (!visited[i]) {
         depthSearch(i);
      }
   }
}
int solve(){
   for (int i = 0; i < m; ++i) {
      int a, b; a = edges[i].first;
      b = edges[i].second;
      G[a].push_back(b);
      G[b].push_back(a);
   }
   bridgeSearch();
   int ans = 0;
   for (int i = 1; i <= n; ++i) {
      for (int j = 1; j <= n; ++j) {
         if (i != j and bridge[i][j]) ans++;
      }
   }
   return ans;
}
int main() {
   n = 5, m = 6;
   edges = {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}};
   cout<< solve();
   return 0;
}

Input

5, 6, {{1, 2}, {1, 3}, {2, 3}, {2, 4}, {2, 5}, {3, 5}}

Output

1