Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ program to find the shortest distance between two nodes in BST
In this article, we are given a BST (binary search tree), and we need to find the shortest distance between 2 given nodes in the BST. Let's have a tree and below are the following scenarios.
Let’s assume some simple input and output scenarios
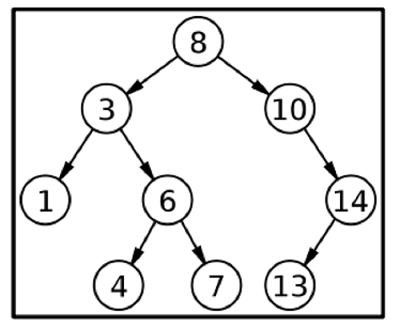
Now we have to find the distances between nodes 4 and 13.
int key1=13, key2=4; res = solve(root, min(key1,key2), max(key1,key2)); output = 6
The shortest distance is 6, which is through 4->6->3->8->10->14->13(the arrows show a path definition and not anything else).
Let’s find another distance from two different nodes in the above figure. Consider the distance from node 7 to node 14. ( 6->3->8->10->14), aslo here the arrows are defining the path. The shortest distance here is 5.
Int key1=7, key2=14; res = solve(root, min(key1,key2), max(key1,key2)); output = 5
So the shortest possible distance in the BST would certainly have the LCA(least common ancestor). So in the given example, the LCA is 8. So we can find the distance of node 4 with 8 and node 13 with 8 and sum it up. So in this problem, we have to find the LCA of the given 2 nodes. Now to find the LCA in a BST, we can check the conditions −
Are both values smaller than the root, then the LCA is on the left side
Are both values greater than the root, then the LCA is on the right side
If one value is smaller and the other is greater, that means this node is the LCA
Algorithm
If in case of binary search tree, finding distance is a bit faster compared to other trees. Following are the Algorithm/steps to be followed to perform the desired task −
Step 1 − A binary search tree and the two nodes are taken as an input, a method is derived to find the distance between these nodes.
Step 2 − The distance is calculated in three cases:
If one node is in the left subtree and the other is in the right subtree, calculate the depth (distance from root to the said node) of the left and add it to the depth of the right node.
If both the nodes are in the left subtree, make the immediate left child of the root as the new root, and calculate the depth of the left node and add it to the depth of the right node with respect to the new root. The root is found recursively until one node is in left subtree and the other is in right subtree.
Similarly, if both the nodes are in the right subtree, make the immediate right child of the root as the new root recursively, and calculate the depth of the left node and add it to the depth of the right node with respect to the new root.
Step 3 − The output achieved will be the distance be the distance between the said nodes.
Example
The following C++ implementation finds the shortest distance between two nodes in a binary search tree −
#include <iostream> using namespace std; class Node { public: int val; Node *left, *right; Node(int val) { this->val = val; left = right = NULL; } }; int distance(Node* root, int val) { if(root->val == val) return 0; else if(root->val > val) return 1+distance(root->left, val); else return 1+distance(root->right, val); } int solve(Node* root, int key1, int key2) { if(root->val > key1 && root->val < key2) { return distance(root, key1) + distance(root, key2); } else if(root->val > key1 && root->val > key2) { return solve(root->left, key1, key2); } else { return solve(root->right, key1, key2); } } int main() { Node* root = new Node(8); root->left = new Node(3); root->right = new Node(10); root->left->left = new Node(1); root->left->right = new Node(6); root->right->right = new Node(14); root->left->right->left = new Node(4); root->left->right->right = new Node(7); root->right->right->left = new Node(13); int key1=13, key2=4; cout << solve(root, min(key1,key2), max(key1,key2)); return 0; }
Output
6
Conclusion
The code assumes that the input is correct and that key1 and key2 are valid. We can have root equals NULL for the invalid input and display a custom message. The algorithm's time complexity is O(h), where h is the tree's height.
616 Views
