Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Queries to find distance between two nodes of a Binary tree – O(logn) method in C++
In this problem, we are given a binary tree and we are given Q queries. Our task is to create a program to solve Queries to find distance between two nodes of a Binary tree – O(logn) method in C++.
Problem Description
In each query, we are given two nodes of the binary tree and we need to find the number distance between two nodes i.e. the number of edges to be traversed to reach one node from another node.
Let’s take an example to understand the problem,
Input: Binary Tree
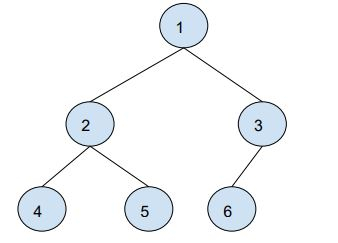
Queries = 3
Q1 -> [2, 6]
Q2 -> [4, 1]
Q3 -> [5, 3]
Output:3, 2, 3
Solution Approach
To solve the problem, we will be using the distance formula which uses the lowest common ancestor(LCA), and their distances.
Distance(n1, n2) = distance(root,n1) + distance(root,n1) - 2 * distance(root,LCA)
To solve the problem to will follow these steps,
Find the levels of each node i.e. N1, N2, LCA.
Then we will find the arrays of the binary tree based on Euler's Tour of the tree.
Then we will create a segment tree for the LCA.
Example
#include <bits/stdc++.h>
#define MAX 1000
using namespace std;
int eulerArray[MAX];
int eIndex = 0;
int vis[MAX];
int L[MAX];
int H[MAX];
int level[MAX];
struct Node {
int data;
struct Node* left;
struct Node* right;
};
struct Node* newNode(int data) {
struct Node* temp = new struct Node;
temp->data = data;
temp->left = temp->right = NULL;
return temp;
}
void FindNodeLevels(struct Node* root) {
if (!root)
return;
queue<pair<struct Node*, int> > q;
q.push({ root, 0 });
pair<struct Node*, int> p;
while (!q.empty()) {
p = q.front();
q.pop();
level[p.first->data] = p.second;
if (p.first->left)
q.push({ p.first->left, p.second + 1 });
if (p.first->right)
q.push({ p.first->right, p.second + 1 });
}
}
void createEulerTree(struct Node* root) {
eulerArray[++eIndex] = root->data;
if (root->left) {
createEulerTree(root->left);
eulerArray[++eIndex] = root->data;
}
if (root->right) {
createEulerTree(root->right);
eulerArray[++eIndex] = root->data;
}
}
void creareEulerArray(int size) {
for (int i = 1; i <= size; i++) {
L[i] = level[eulerArray[i]];
if (vis[eulerArray[i]] == 0) {
H[eulerArray[i]] = i;
vis[eulerArray[i]] = 1;
}
}
}
pair<int, int> seg[4 * MAX];
pair<int, int> min(pair<int, int> a, pair<int, int> b) {
if (a.first <= b.first)
return a;
else
return b;
}
pair<int, int> buildSegTree(int low, int high, int pos) {
if (low == high) {
seg[pos].first = L[low];
seg[pos].second = low;
return seg[pos];
}
int mid = low + (high - low) / 2;
buildSegTree(low, mid, 2 * pos);
buildSegTree(mid + 1, high, 2 * pos + 1);
seg[pos] = min(seg[2 * pos], seg[2 * pos + 1]);
}
pair<int, int> LCA(int qlow, int qhigh, int low, int high, int pos) {
if (qlow <= low && qhigh >= high)
return seg[pos];
if (qlow > high || qhigh < low)
return { INT_MAX, 0 };
int mid = low + (high - low) / 2;
return min(LCA(qlow, qhigh, low, mid, 2 * pos), LCA(qlow, qhigh,mid + 1, high, 2 * pos +1));
}
int CalcNodeDistance(int node1, int node2, int size) {
int prevn1 = node1, prevn2 = node2;
node1 = H[node1];
node2 = H[node2];
if (node2 < node1)
swap(node1, node2);
int lca = LCA(node1, node2, 1, size, 1).second;
lca = eulerArray[lca];
return level[prevn1] + level[prevn2] - 2 * level[lca];
}
int main() {
int N = 6;
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
FindNodeLevels(root);
createEulerTree(root);
creareEulerArray(2 * N - 1);
buildSegTree(1, 2 * N - 1, 1);
int Q = 4;
int query[Q][2] = {{1, 5}, {4, 6}, {3, 4}, {2, 4} };
for(int i = 0; i < Q; i++)
cout<<"The distance between two nodes of binary tree is "<<CalcNodeDistance(query[i][0], query[i][1], 2 * N - 1)<<endl;
return 0;
}Output
The distance between two nodes of binary tree is 2 The distance between two nodes of binary tree is 4 The distance between two nodes of binary tree is 3 The distance between two nodes of binary tree is 1
100 Views
