Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find the shortest distance between any pair of two different good nodes in C++
Suppose we have a given weighted undirected graph with N different nodes and M edges, some of the nodes are good nodes. We have to find the shortest distance between any pair of two different good nodes. In the given diagram the yellow in the following graph are considered to be good nodes.
So, if the input is like
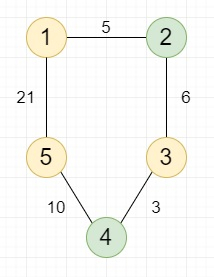
then the output will be 11, as the pairs of good nodes and distance between them are: (1 to 3) the distance is 11, (3 to 5) the distance is 13, (1 to 5) the distance is 24, out of which 11 is the minimum.
To solve this, we will follow these steps −
N := 100005
MAX_VAL := 99999999
create one priority queue q
result := MAX_VAL
for initialize i := 1, when i <= n, update (increase i by 1), do −
if good_verts[i] is false, then −
Ignore following part, skip to the next iteration
for initialize j := 1, when j <= n, update (increase j by 1), do −
dist[j] := MAX_VAL
vis[j] := 0
dist[i] := 0
while (not q is empty), do −
delete element from q
insert { 0, i } into q
good := 0
while (not q is empty), do −
v := top element of q
delete element from q
if vis[v] is true, then −
Ignore following part, skip to the next iteration
vis[v] := 1
good := good + (1 when good_verts[v] is true, otherwise 0)
if dist[v] > result, then −
Come out from the loop
if good is same as 2 and good_verts[v], then −
result := minimum of result and dist[v]
Come out from the loop
for initialize j := 0, when j < size of graph[v], update (increase j by 1), do −
to := graph[v, j].first
weight := graph[v, j].second
if dist[v] + weight < dist[to], then −
dist[to] := dist[v] + weight
insert { dist[to], to } into q
return result
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
#define N 100005
#define MAX_VAL 99999999
void insert_edge(vector<pair<int, int> > graph[], int x, int y, int weight) {
graph[x].push_back({ y, weight });
graph[y].push_back({ x, weight });
}
int get_min_dist(vector<pair<int, int> > graph[], int n, int dist[], int vis[], int good_verts[], int k) {
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int>>> q;
int result = MAX_VAL;
for (int i = 1; i <= n; i++) {
if (!good_verts[i])
continue;
for (int j = 1; j <= n; j++) {
dist[j] = MAX_VAL;
vis[j] = 0;
}
dist[i] = 0;
while (!q.empty())
q.pop();
q.push({ 0, i });
int good = 0;
while (!q.empty()) {
int v = q.top().second;
q.pop();
if (vis[v])
continue;
vis[v] = 1;
good += good_verts[v];
if (dist[v] > result)
break;
if (good == 2 and good_verts[v]) {
result = min(result, dist[v]);
break;
}
for (int j = 0; j < graph[v].size(); j++) {
int to = graph[v][j].first;
int weight = graph[v][j].second;
if (dist[v] + weight < dist[to]) {
dist[to] = dist[v] + weight;
q.push({ dist[to], to });
}
}
}
}
return result;
}
int main() {
int n = 5, m = 5;
vector<pair<int, int> > graph[N];
insert_edge(graph, 1, 2, 3);
insert_edge(graph, 1, 2, 3);
insert_edge(graph, 2, 3, 4);
insert_edge(graph, 3, 4, 1);
insert_edge(graph, 4, 5, 8);
int k = 3;
int good_verts[N], vis[N], dist[N];
good_verts[1] = good_verts[3] = good_verts[5] = 1;
cout << get_min_dist(graph, n, dist, vis, good_verts, k);
}Input
n = 5, m = 5 insert_edge(graph, 1, 2, 3); insert_edge(graph, 1, 2, 3); insert_edge(graph, 2, 3, 4); insert_edge(graph, 3, 4, 1); insert_edge(graph, 4, 5, 8); k = 3 good_verts[1] = good_verts[3] = good_verts[5] = 1;
Output
7
345 Views
