
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count pairs from two BSTs whose sum is equal to a given value x in C++
We are given two binary search trees as input and a variable x. The goal is to find pairs of nodes from each tree such that the sum of value of nodes is equal to x. Take node 1 from BST_1 and node 2 from BST_2 and add data part of both. If sum=x. Increment count.
Let us understand with examples.
Input
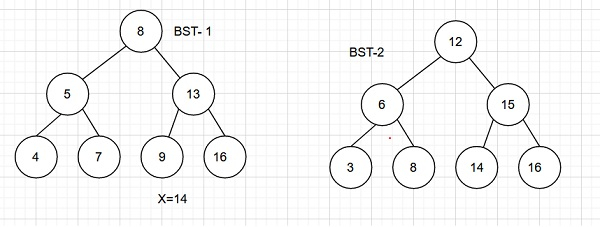
Output − Count of pairs from two BSTs whose sum is equal to a given value x are − 1
Explanation − The pair is (8,6)
Input
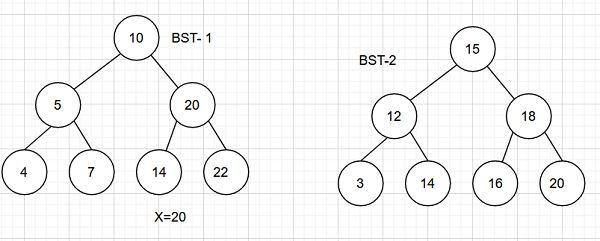
Output −Count of pairs from two BSTs whose sum is equal to a given value x are − 2
Explanation − The pairs are (5,15) and (4,16)
Approach used in the below program is as follows
In this approach we will traverse the BST’s using an iterative inorder method. Traverse BST 1 from smallest node to largest using iterative inorder method and traverse BST 2 from reverse of iterative inorder method. Take the sum of current nodes of both BST’s. If sum is x increment count. If sum>x then move to the inorder predecessor of the current node in BST 2. If sum<x then move to the inorder predecessor of the current node in BST 1.
Take two trees BST_1 and BST_2 having integer data part and left, right pointers to child nodes.
Function insert_node(int data) inserts a new node to the Tree with data and returns a pointer to it.
Create both BSTs using inser_node() and pass to BST_sum_x(Tree* BST_1, Tree* BST_2, int x).
Function BST_sum_x(Tree* BST_1, Tree* BST_2, int x) takes root nodes of both trees and returns the count of pairs of nodes with sum of data part as x.
Take the initial count as 0 for the number of pairs with sum x.
For iterative inorder traversals take two variables Tree* stack_top_1, *stack_top_2;
Create two stacks stack stack_1, stack_2;
Now start outer while loop.
Go to leftmost (smallest) node of BST_1 using while loop and push all nodes to stack_1
Go to rightmost (greatest) node of BST_2 using while loop and push all nodes to stack_2
If any of the stacks is empty break the outer while loop.
Take the top nodes of both stacks and add their data parts and store in temp.
If temp ( sum) == x then increment count. Remove top elements from both stack_1 and stack_2 using pop operation.
Set BST_1=stack_1->right and BST_2=stack_2->left ( next successor in BST_1 and predecessor in BST_2 )
If temp<x then only remove top from stack_1 and move to the next successor in BST_1.
IF temp>x then only remove top from stack_2 and move to the next predecessor in BST_1.
At the end of outer while, count has a number of pairs with node’s of both BSTs having sum x.
Return count as result.
Example
#include <bits/stdc++.h>
using namespace std;
struct Tree{
int data;
Tree* left, *right;
};
Tree* insert_node(int data){
Tree* newNode = (Tree*)malloc(sizeof(Tree));
newNode->data = data;
newNode->left = NULL;
newNode->right = NULL;
}
int BST_sum_x(Tree* BST_1, Tree* BST_2, int x){
int count = 0;
Tree* stack_top_1, *stack_top_2;
stack<Tree*> stack_1, stack_2;
if (BST_1 == NULL || BST_2 == NULL){
return 0;
}
while (1){
while (BST_1 != NULL){
stack_1.push(BST_1);
BST_1 = BST_1->left;
}
while (BST_2 != NULL){
stack_2.push(BST_2);
BST_2 = BST_2->right;
}
if (stack_1.empty() || stack_2.empty()){
break;
}
stack_top_1 = stack_1.top();
stack_top_2 = stack_2.top();
int temp = stack_top_1->data + stack_top_2->data;
if (temp == x){
count++;
stack_1.pop();
stack_2.pop();
BST_1 = stack_top_1->right;
BST_2 = stack_top_2->left;
}
else if (temp < x){
stack_1.pop();
BST_1 = stack_top_1->right;
}
else{
stack_2.pop();
BST_2 = stack_top_2->left;
}
}
return count;
}
int main(){
//BST 1
Tree* BST_1 = insert_node(15);
BST_1->left = insert_node(10);
BST_1->right = insert_node(8);
BST_1->left->left = insert_node(12);
BST_1->left->right = insert_node(24);
BST_1->right->left = insert_node(16);
//BST 2
Tree* BST_2 = insert_node(20);
BST_2->left = insert_node(16);
BST_2->right = insert_node(4);
BST_2->left->left = insert_node(18);
BST_2->left->right = insert_node(28);
BST_2->right->left = insert_node(22);
int x = 28;
cout<<"Count of pairs from two BSTs whose sum is equal to a given value x ar: "<<BST_sum_x(BST_1, BST_2, x);
return 0;
}
Output
If we run the above code it will generate the following output −
Count of pairs from two BSTs whose sum is equal to a given value x ar: 1

