Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points in C++
We are given a circle with K equidistant points on its circumference. Also we are given two points A and B. The goal is to count the number of triangles possible using these points such that they have an obtuse angle ACB( angle greater than 90o) inside them. The points A and B are such that A < B.
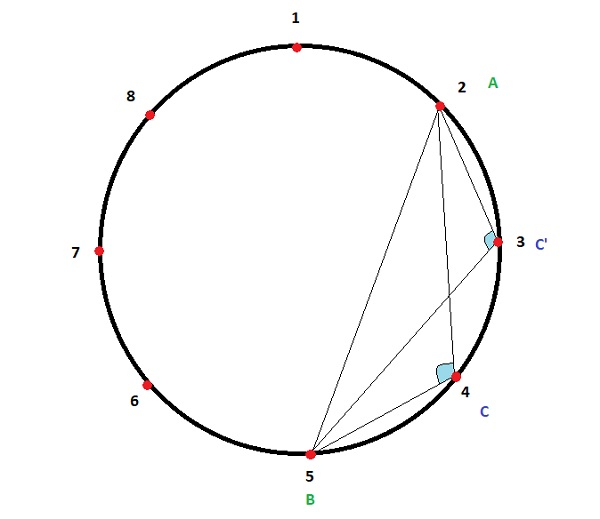
Here K=8, A=2, B=5, count of points=2 (C,C’) such that angle LACB, LAC’B are obtuse.
Let us understand with examples
Input − k=10, A=2, B=4
Output − Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points are − 1
Explanation − The point will be C=3
Input − k=12, A=2, B=10
Output − Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points are − 3
Approach used in the below program is as follows
It can be seen that if the smaller the arc between A and B the points will lie on that arc only.
Calculate both arcs and if they are of equal length then no such triangle possible, return 0. Else set count as smaller arc which is distance in terms of points.
Take input as integers k, point_a and point_b.
Function Obtuse_angle_circle(int point_a, int point_b, int k) takes all variables and returns count of obtuse angles in a circle with ‘k' equidistant points between 2 given points
Take the initial count as 0.
Calculate the first arc as arc_1 = (point_b - point_a) - 1. (b>a)
Calculate the second arc as (k - point_b) + (point_a - 1).
If both arcs are equal then return 0 as no such points possible.
If they are unequal then update count as minimum of two as all points lie on it.
Return count as result.
Example
#include <bits/stdc++.h>
using namespace std;
int Obtuse_angle_circle(int point_a, int point_b, int k){
int count = 0;
int arc_1 = (point_b - point_a) - 1;
int arc_2 = (k - point_b) + (point_a - 1);
if (arc_1 == arc_2){
return 0;
}
count = min(arc_1, arc_2);
return count;
}
int main(){
int k = 10;
int point_a= 1;
int point_b = 4;
cout<<"Count of obtuse angles in a circle with ‘k' equidistant points between 2 given pointsare: "<<Obtuse_angle_circle(point_a, point_b, k);
return 0;
}Output
If we run the above code it will generate the following output −
Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points are: 2
80 Views
