
- Digital Electronics - Home
- Digital Electronics Basics
- Types of Digital Systems
- Types of Signals
- Logic Levels And Pulse Waveforms
- Digital System Components
- Digital Logic Operations
- Digital Systems Advantages
- Number Systems
- Number Systems
- Binary Numbers Representation
- Binary Arithmetic
- Signed Binary Arithmetic
- Octal Arithmetic
- Hexadecimal Arithmetic
- Complement Arithmetic
- Base Conversions
- Base Conversions
- Binary to Decimal Conversion
- Decimal to Binary Conversion
- Binary to Octal Conversion
- Octal to Binary Conversion
- Octal to Decimal Conversion
- Decimal to Octal Conversion
- Hexadecimal to Binary Conversion
- Binary to Hexadecimal Conversion
- Hexadecimal to Decimal Conversion
- Decimal to Hexadecimal Conversion
- Octal to Hexadecimal Conversion
- Hexadecimal to Octal Conversion
- Binary Codes
- Binary Codes
- 8421 BCD Code
- Excess-3 Code
- Gray Code
- ASCII Codes
- EBCDIC Code
- Code Conversion
- Error Detection & Correction Codes
- Logic Gates
- Logic Gates
- AND Gate
- OR Gate
- NOT Gate
- Universal Gates
- XOR Gate
- XNOR Gate
- CMOS Logic Gate
- OR Gate Using Diode Resistor Logic
- AND Gate vs OR Gate
- Two Level Logic Realization
- Threshold Logic
- Boolean Algebra
- Boolean Algebra
- Laws of Boolean Algebra
- Boolean Functions
- DeMorgan's Theorem
- SOP and POS Form
- POS to Standard POS Form
- Minimization Techniques
- K-Map Minimization
- Three Variable K-Map
- Four Variable K-Map
- Five Variable K-Map
- Six Variable K-Map
- Don't Care Condition
- Quine-McCluskey Method
- Min Terms and Max Terms
- Canonical and Standard Form
- Max Term Representation
- Simplification using Boolean Algebra
- Combinational Logic Circuits
- Digital Combinational Circuits
- Digital Arithmetic Circuits
- Multiplexers
- Multiplexer Design Procedure
- Mux Universal Gate
- 2-Variable Function Using 4:1 Mux
- 3-Variable Function Using 8:1 Mux
- Demultiplexers
- Mux vs Demux
- Parity Bit Generator and Checker
- Comparators
- Encoders
- Keyboard Encoders
- Priority Encoders
- Decoders
- Arithmetic Logic Unit
- 7-Segment LED Display
- Code Converters
- Code Converters
- Binary to Decimal Converter
- Decimal to BCD Converter
- BCD to Decimal Converter
- Binary to Gray Code Converter
- Gray Code to Binary Converter
- BCD to Excess-3 Converter
- Excess-3 to BCD Converter
- Adders
- Half Adders
- Full Adders
- Serial Adders
- Parallel Adders
- Full Adder using Half Adder
- Half Adder vs Full Adder
- Full Adder with NAND Gates
- Half Adder with NAND Gates
- Binary Adder-Subtractor
- Subtractors
- Half Subtractors
- Full Subtractors
- Parallel Subtractors
- Full Subtractor using 2 Half Subtractors
- Half Subtractor using NAND Gates
- Sequential Logic Circuits
- Digital Sequential Circuits
- Clock Signal and Triggering
- Latches
- Shift Registers
- Shift Register Applications
- Binary Registers
- Bidirectional Shift Register
- Counters
- Binary Counters
- Non-binary Counter
- Design of Synchronous Counter
- Synchronous vs Asynchronous Counter
- Finite State Machines
- Algorithmic State Machines
- Flip Flops
- Flip-Flops
- Conversion of Flip-Flops
- D Flip-Flops
- JK Flip-Flops
- T Flip-Flops
- SR Flip-Flops
- Clocked SR Flip-Flop
- Unclocked SR Flip-Flop
- Clocked JK Flip-Flop
- JK to T Flip-Flop
- SR to JK Flip-Flop
- Triggering Methods:Flip-Flop
- Edge-Triggered Flip-Flop
- Master-Slave JK Flip-Flop
- Race-around Condition
- A/D and D/A Converters
- Analog-to-Digital Converter
- Digital-to-Analog Converter
- DAC and ADC ICs
- Realization of Logic Gates
- NOT Gate from NAND Gate
- OR Gate from NAND Gate
- AND Gate from NAND Gate
- NOR Gate from NAND Gate
- XOR Gate from NAND Gate
- XNOR Gate from NAND Gate
- NOT Gate from NOR Gate
- OR Gate from NOR Gate
- AND Gate from NOR Gate
- NAND Gate from NOR Gate
- XOR Gate from NOR Gate
- XNOR Gate from NOR Gate
- NAND/NOR Gate using CMOS
- Full Subtractor using NAND Gate
- AND Gate Using 2:1 MUX
- OR Gate Using 2:1 MUX
- NOT Gate Using 2:1 MUX
- Memory Devices
- Memory Devices
- RAM and ROM
- Cache Memory Design
- Programmable Logic Devices
- Programmable Logic Devices
- Programmable Logic Array
- Programmable Array Logic
- Field Programmable Gate Arrays
- Digital Electronics Families
- Digital Electronics Families
- CPU Architecture
- CPU Architecture
Gray Code to Binary Converter
A gray code-to-binary converter is a digital circuit that can translate a gray code into an equivalent pure binary code. Thus, a gray code to binary converter takes a gray code as input and gives a pure binary code as output.
The truth table of a 3-bit gray code to binary code converter is given below −
| Gray Code | Binary Code | ||||
|---|---|---|---|---|---|
| G2 | G1 | G0 | B2 | B1 | B0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Let us obtain the Boolean expression for the binary output bits. For this, we will simplify the truth table using the K-map technique.
K-Map for Binary Bit B0
The K-map simplification for the binary output bit B0 is shown in the following figure.
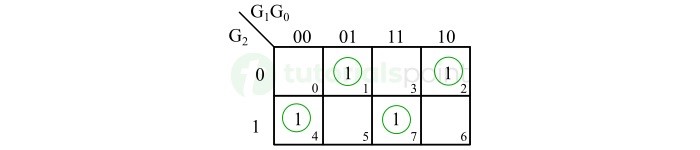
The Boolean expression for the binary bit B0 will be,
$$\mathrm{B_{0} \: = \: \overline{G_{2}} \: \overline{G_{1}} \: G_{0} \: + \: \overline{G_{2}} \: G_{1} \: \overline{G_{0}} \: + \: G_{2} \: \overline{G_{1}} \: \overline{G_{0}}\: + \: G_{2} \: G_{1} \: G_{0}}$$
We can further simplify this expression as follows,
$$\mathrm{\Rightarrow \: B_{0} \: = \: \overline{G_{2}} \: (\overline{G_{1}} \: G_{0} \: + \: G_{1} \: \overline{G_{0}}) \: + \: G_{2} \: (\overline{G_{1}} \: \overline{G_{0}}\: + \: G_{1} \: G_{0})}$$
$$\mathrm{\Rightarrow \: B_{0} \: = \: \overline{G_{2}} \: ( G_{0} \: \oplus \: G_{1}) \: + \: G_{2} \: \overline{(G_{0} \: \oplus \: G_{1})}}$$
$$\mathrm{B_{0} \: = \: G_{0} \: \oplus \: G_{1} \: \oplus \: G_{2}}$$
This is the simplified expression for the binary bit B0.
K-Map for Binary Bit B1
The K-map simplification for the binary output B1 is shown below.
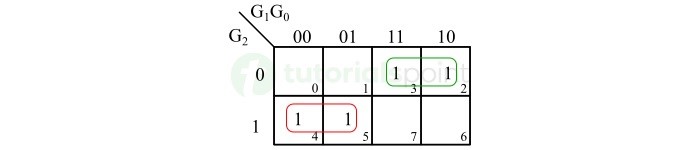
The Boolean expression for the binary bit B1 is,
$$\mathrm{B_{1} \: = \: G_{2} \: \overline{G_{1}} \: + \: \overline{G_{2}} \: G_{1} \: = \: G_{1} \: \oplus \: G_{2}}$$
K-Map for Binary Bit B2
The following figure shows the K-map simplification for the binary bit B2.
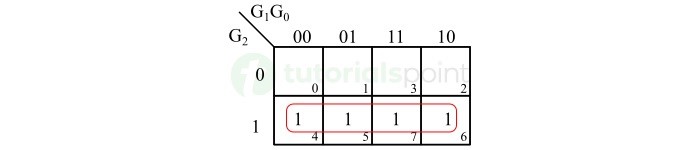
From this K-Map, we obtain the following Boolean expression −
$$\mathrm{B_{2} \: = \: G_{2}}$$
The logic circuit implementation of this 3-bit gray to binary code converter is shown in the following figure.
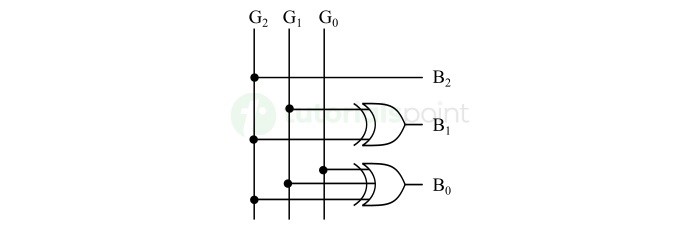
This logic circuit can translate a 3-bit gray code into an equivalent 3-bit binary code. We can also follow the same procedure to implement a gray code to binary code converter for any number of bits.