Circuit Rank

Let 'G' be a connected graph with 'n' vertices and 'm' edges. A spanning tree 'T' of G contains (n-1) edges.

Therefore, the number of edges you need to delete from 'G' in order to get a spanning tree = m-(n-1), which is called the circuit rank of G.

This formula is true, because in a spanning tree you need to have 'n-1' edges. Out of 'm' edges, you need to keep 'n–1' edges in the graph.

Hence, deleting 'n–1' edges from 'm' gives the edges to be removed from the graph in order to get a spanning tree, which should not form a cycle.

Example

Take a look at the following graph −

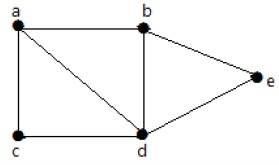
For the graph given in the above example, you have m=7 edges and n=5 vertices.

Then the circuit rank is

G = m – (n – 1)
= 7 – (5 – 1)
= 3

Example

Let 'G' be a connected graph with six vertices and the degree of each vertex is three. Find the circuit rank of 'G'.

By the sum of degree of vertices theorem,

6 × 3 = 2|E|

|E| = 9

Circuit rank = |E| – (|V| – 1)

= 9 – (6 – 1) = 4

Mahesh Parahar

e

Updated on: 23-Aug-2019

673 Views

Kickstart Your Career

Get certified by completing the course

Get Started