Prescriptive Analytics - Optimization Techniques

---

---

Prescriptive analytics is a subset of data analytics that employs prediction models to recommend actions for optimal results. Prescriptive Analytics demonstrates how to utilize analytics to make better decisions based on facts.

For example, predictive analytics includes forecasting the heavy rain in a city over the next 24 hours, whereas predictive analytics involves answering questions about how to manage the situation with optimal resources. Prescriptive analytics relies on optimization and rule-based decision-making strategies.

Optimization techniques such as linear programming, integer programming, and nonlinear programming are significant in prescriptive analytics because they allow a set of decisions to be made optimally. These strategies are used in a model that reflects the decisions to be made, the limitations of the decisions, and a metric for comparing the decisions.

Prescriptive analytics makes use of optimization and rules-based strategies to assist in making better data-driven judgments. Linear and nonlinear optimizations are essential techniques in prescriptive analytics, helping organizations make data-driven decisions.

1. Linear Programming

Linear optimization involves mathematical methods used to optimize a linear objective function, subject to linear equality and inequality constraints. It is used to solve problems with linear constraints and objectives. The process involves defining a model that represents business reality, including all limitations and constraints. The model is then validated to ensure it reflects business realities. Linear optimization techniques are most widely used in Supply chain management, production planning, transportation, finance, and workforce scheduling.

Key Components of Linear Programming

• Objective Function − A linear function that needs to be maximized or minimized (e.g., profit, cost). The objective function is a linear equation that describes the relationship between a decision variable and the outcome to be optimized. For example - Maximize Z = c₁x₁+c₂x₂+...+c_nx_n Where Z is the objective to be maximized, x₁,x₂,...,x_n are decision variables, and c₁,c₂,...,c_n are the coefficients.
• Decision Variables − Variables that are controlled or optimized to achieve the optimal solution. In Prescriptive Analytics, these decision variables may indicate the number of products to generate resource allocation or product distribution.
• Constraints − Linear equations or inequalities that constrain the values of decision variables. These restrictions are represented as linear inequalities or equality. For example: a₁x₁+a₂x₂+...+a_nx_n≤b where b is the upper limit, and a₁, a2,..., a_n are the coefficients that reflect the contribution of each variable.
• Feasible Region − The feasible region consists of all viable solutions that meet the constraints. It is usually a convex polyhedron in multidimensional space. Any point in this region can be used to solve the optimization problem.
• Optimization Solution − The purpose is to identify the location in the feasible zone that maximizes or reduces the objective function. This is accomplished through the use of techniques like the Simplex Method and Interior-Point Methods.

Linear Optimization

Optimisation is employed in all aspects of the company, including operations, finance, human resources, and marketing. Assume you manage a small paper manufacturing unit and need to determine how much paper production is required. Of course, you can choose your product demand. To improve sales and scale up a product, it's important to do research and evaluate aspects like demand and costs.

If a company has facilities that produce hundreds of products every day, data is essential for optimizing the product mix. This optimization is not intended to make production processes faster or cheaper. We are interested in how much we need to generate.

Some of the common applications for linear optimization are −

• Product Mix − Choosing the appropriate quantity of each product for production and sales.
• Planning − Choosing when to produce products based on supply/demand estimates, such as during the holiday sales season.
• Plan Investment Portfolio − Consider investment options to maximize return or minimize risk exposure, within specified limits.
• Optimizing labour allocation − How to schedule employees' shifts?
• Optimizing transportation and supply chain − routes to reduce wait times. How to get products from suppliers to warehouses to distributors, particularly for perishable goods.

Steps in Linear Optimization

Applications of Linear Optimization

Some of the key application areas of Linear Optimization are as follows -

• Supply chain optimization − By using optimization models, companies can optimize their supply chain processes, including but not limited to inventory management, transportation planning and production scheduling.
• Staff scheduling − Hospitals can utilize an optimization model to find the best schedule for nurses and doctors, taking into consideration shift preferences, task allocation, and workload regulations.
• Portfolio Optimization − Financial institutions utilize optimization models to identify the best allocation of funds among multiple investment possibilities, taking into account risk, return, and asset correlation.
• Vehicle Routing − An optimization model can be used to optimize truck routing and scheduling, taking into account factors such as road congestion, delivery windows, and vehicle capacity.
• Production Planning − An optimization model can be used to calculate the ideal production schedule, taking into account aspects such as production capacity, raw material availability, and production costs.

2. Nonlinear programming

Nonlinear programming includes minimizing or maximizing a nonlinear objective function under bound constraints, linear constraints, or nonlinear constraints, which can be inequalities or equalities. Typical engineering challenges include examining design tradeoffs, selecting optimal designs, computing optimal trajectories, and portfolio optimization and model calibration in computational finance. Nonlinear optimization is concerned with problems in which the objective function or any of the constraints are nonlinear. It is used to address issues that have nonlinear objectives or constraints. For example, a company may utilize nonlinear optimization techniques to find the optimum approach to allocate advertising money across numerous media; engineering design, portfolio optimization, machine learning, and other scientific domains.

Non-linear Optimization

Non-linear Optimization in Prescriptive Analytics works using the following methods −

Objective Function

The goal function in Non-linear Optimization could be a nonlinear equation that you wish to maximize (e.g., profit, efficiency) or minimize (e.g., cost, error). For example −

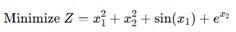
The relationship between decision variables 1, 2 and the outcome is not a straight line. Small changes in decision variables may result in complex changes in the outcome.

Decision Variables

Variables that are controlled or optimized to achieve the optimal solution. In Prescriptive Analytics, these decision variables may indicate the number of products to generate resource allocation or product distribution.

Non-linear Constraints

Non-linear constraints are inequalities or equalities that do not have a linear relationship with the decision variables. For example

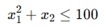
These restrictions may include powers, exponentials, logarithms, or other non-linear functions, making the feasible region more complex than in linear issues.

Feasible Region

The feasible region consists of all viable solutions that meet the constraints. It is usually a convex polyhedron in multidimensional space. Any point in this region can be used to solve the optimization problem. The viable region in nonlinear optimization may have complex boundaries and not be a simple convex polyhedron as in Linear Optimization. Non-convex regions can have several local optima (peaks and valleys), which means that while many locations appear optimal in specific areas, only one is truly the global optimum.

Non-convex Problems

Non-convex problems are common in nonlinear optimization. Non-convex issues, as opposed to convex problems, might have several local optima, necessitating the use of specialized techniques to find the global optimum.

Optimization Solution

The purpose is to identify the location in the feasible zone that maximizes or reduces the objective function. This is accomplished through the use of techniques like the Simplex Method and Interior-Point Methods.

Applications of Non-linear Optimization

Some of the key applications or use cases of Non-linear Optimization are as follows −

• Pricing Optimization − NLO assists organizations with non-linear demand curves in determining the most effective pricing methods to maximize revenues. Demand for items does not always drop linearly with price, hence nonlinear models are required to accurately reflect this tendency.
• Supply Chain Optimization − Non-linear cost structures can exist in logistics (for example, economies of scale or transit routes). NLO aids in the determination of optimal resource allocation while accounting for non-linear cost functions.
• Portfolio Optimization − In finance, NLO is used to manage risk and return in investment portfolios with non-linear connections. One typical example is optimizing a portfolio based on asset return variance (a quadratic function).
• Health Care − NLO can be used to optimize treatment plans based on the non-linear relationships between various treatments, patient outcomes, and costs. For example, a hospital could utilize it to reduce operating costs while taking into account non-linear risks associated with treatment outcomes.
• Machine Learning Model Training − Non-linear optimization is widely used in machine learning to train models like neural networks, where the cost functions are often non-linear.

3. Integer Programming (IP) or Integer Optimization (IO)

Integer Optimization (IO), sometimes known as Integer Programming (IP), is a type of optimization in which decision variables store integer values. Integer programming is an optimization technique used in prescriptive analytics to identify the optimum solution to a problem using integer variables, often known as whole numbers. The goal is to increase profit while reducing costs and resources. This makes it especially effective in situations where decisions are based on "yes/no" decisions, or where numbers cannot be fractional (e.g., items, people, and machines). In Prescriptive Analytics, integer optimization aids in making optimal or near-optimal decisions under such limitations.

How does Integer Optimization work?

The working of Integer optimization is based on the following concepts −

• Objective Function − The main goal of this function is to maximize or reduce a specific function (e.g., profit, cost, time), but using integer choice variables. For example - Maximize Z = c₁x₁+c₂x₂+...+c_nx_n Where Z is the objective to be maximized, x₁,x₂,...,x_n are integer decision variables, and c₁,c₂,...,c_n are the coefficients.
• Constraints − The constraints are linear inequalities or equalities, but some or all of the decision variables have to be integers. For example: a₁x₁+a₂x₂+...+a_nx_n≤b where x₁,x₂,...,x_n are integer decision variables.

Applications of Integer Optimization

Some of the key applications of Integer Optimization concerning Prescriptive Analytics are as follows −

• Supply Chain Management − Optimize production, transportation, and distribution while taking into account specific variables such as the number of trucks, factories, or warehouses.
• Workforce Scheduling − Optimize staff allocation or shift assignments while adhering to legal requirements, employee availability, and demand.
• Capital Budgeting − Allocate a fixed budget to numerous initiatives, with each project requiring a specific investment amount (for example, fixed costs).
• Portfolio Optimization − Choose an investment portfolio that optimizes return while minimizing risk, given the requirement that certain investment amounts be discrete.
• Network Design and Optimization − Optimize the architecture of communication, transportation, or utility networks while keeping the number of facilities, connections, or resources discrete.
• Production and Manufacturing Planning − Optimize production schedules, machine utilization, or resource allocation using integer limitations.
• Facility Location Planning − Optimize the quantity and location of facilities (e.g., warehouses, factories, retail stores) where decisions need distinct choices.
• Transportation and Logistics Optimization − Makes specific decisions to reduce transportation costs or time (for example, the number of vehicles, routes, or deliveries).
• Healthcare Resource Allocation − Optimize the allocation of resources like doctors, nurses, and medical equipment where decisions must be made in large numbers.