Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Bellman Ford Algorithm in C++?
Bellman Ford Algorithm is dynamic programming algorithm which is used to find the shortest path of any vertex computed from a vertex treated as starting vertex. this algorithm follows iterative method and continuously tries to find shortest Path. The Bellman Ford Algorithm on weighted graph.
this algorithm was proposed by Alphonso shimbel in 1955. The algorithm has revisions by Richard Bellman and Lester Ford in the year 1956 and 1958, due to this algorithm was named Bellman Ford Algorithm. This algorithm was also revised by Eward F. Moore in 1957, which made its name to Bellman-Ford-Moore Algorithm.
This algorithm is better as it can handle edge’s with negative weights. Though the algorithm is slower than Dijkstra’s algorithm, it is a better one as it handles more versatile type of graphs.
Algorithm
Input : weighted graph and starting vertex Output : shortest distance between all vertices from the src. For negative weight cycle, the same will be returned as the weight cannot be calculated.
Algorithm
Step 1 : This is the initialisation step, an array is created that stores the distance of all vertices from the initial vertex. The array say dist[] of size equal to the number of vertices in the graph. Step 2 : Calculate the shortest distance of vertex. Loop through step 3 for n-1 number of times ( n is the number of vertices of graph). Step 3 : Follow following steps for each edge i-j Step 3.1 : If dist[v] > dist[u] + weight[uv]. Then, dist[v] = dist[u] + weight[uv]. Step 4 : Check and flag if there is any negative cycle. If step 3.1 executes then there is a negative cycle.
Negative Cycle : If there exists a path shorter than the regular edge traversal, there is a negative cycle.
Example
Let’s learn more about the algorithm by solving some graph related problems.
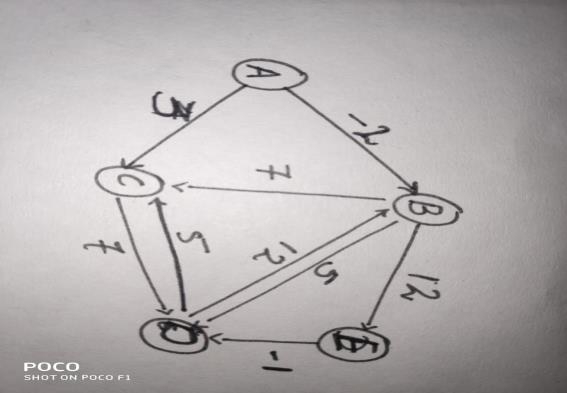
You can see all the vertices and edges of the graph along with the weights associated to them.
Lets find the shortest distance between vertex A and vertex E using Bellman-ford Algorithm.
Set the source vertex (A) to zero 0 and set the rest distances to infinity ∞.
A B C D E 0 ∞ ∞ ∞ ∞
Checking weight of edge A-B and then A-C,
For A- B we have only one path but for A-C, we have two paths that can be traversed and we will check which one is the shortest.
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ - for (A-B) 0 -2 3 ∞ ∞ - for (A-C)
For the next to vertices, we will calculate and the shortest distances for the initial vertex.
A B C D E 0 ∞ ∞ ∞ ∞ 0 -2 ∞ ∞ ∞ 0 -2 3 3 10
The shortest distance hence using the algorithm is 10. Traversing the path A-B-E . Using this we also found that there is a negative cycle.
Example
#include <bits/stdc++.h>
struct Edge {
int src, dest, weight;
};
struct Graph {
int V, E;
struct Edge* edge;
};
struct Graph* createGraph(int V, int E) {
struct Graph* graph = new Graph;
graph->V = V;
graph->E = E;
graph->edge = new Edge[E];
return graph;
}
void BellmanFord(struct Graph* graph, int src) {
int V = graph->V;
int E = graph->E;
int dist[V];
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;
dist[src] = 0;
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
int u = graph->edge[j].src;
int v = graph->edge[j].dest;
int weight = graph->edge[j].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v])
dist[v] = dist[u] + weight;
}
}
for (int i = 0; i < E; i++) {
int u = graph->edge[i].src;
int v = graph->edge[i].dest;
int weight = graph->edge[i].weight;
if (dist[u] != INT_MAX && dist[u] + weight < dist[v]) {
printf("Graph contains negative weight cycle");
return;
}
}
printf("Vertex :\t\t\t ");
for (int i = 0; i < V; ++i)
printf("%d \t", i);
printf("\nDistance From Source : ");
for (int i = 0; i < V; ++i)
printf("%d \t",dist[i]);
return;
}
int main() {
int V = 5;
int E = 8;
struct Graph* graph = createGraph(V, E);
graph->edge[0].src = 0;
graph->edge[0].dest = 1;
graph->edge[0].weight = -1;
graph->edge[1].src = 0;
graph->edge[1].dest = 2;
graph->edge[1].weight = 4;
graph->edge[2].src = 1;
graph->edge[2].dest = 2;
graph->edge[2].weight = 3;
graph->edge[3].src = 1;
graph->edge[3].dest = 3;
graph->edge[3].weight = 2;
graph->edge[4].src = 1;
graph->edge[4].dest = 4;
graph->edge[4].weight = 2;
graph->edge[5].src = 3;
graph->edge[5].dest = 2;
graph->edge[5].weight = 5;
graph->edge[6].src = 3;
graph->edge[6].dest = 1;
graph->edge[6].weight = 1;
graph->edge[7].src = 4;
graph->edge[7].dest = 3;
graph->edge[7].weight = -3;
BellmanFord(graph, 0);
return 0;
}Output
Vertex : 0 1 2 3 4 Distance From Source : 0 -1 2 -2 1
4K+ Views
