Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Bellman–Ford Algorithm for Shortest Paths
Bellman-Ford algorithm is used to find minimum distance from the source vertex to any other vertex. The main difference between this algorithm with Dijkstra’s the algorithm is, in Dijkstra’s algorithm we cannot handle the negative weight, but here we can handle it easily.
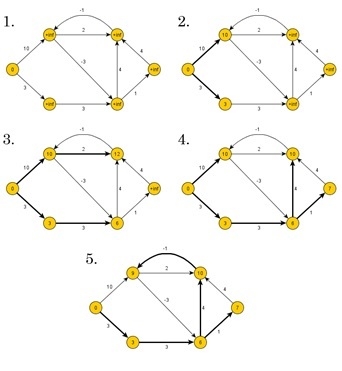
Bellman-Ford algorithm finds the distance in a bottom-up manner. At first, it finds those distances which have only one edge in the path. After that increase the path length to find all possible solutions.
Input and Output
Input: The cost matrix of the graph: 0 6 ∞ 7 ∞ ∞ 0 5 8 -4 ∞ -2 0 ∞ ∞ ∞ ∞ -3 0 9 2 ∞ 7 ∞ 0 Output: Source Vertex: 2 Vert: 0 1 2 3 4 Dist: -4 -2 0 3 -6 Pred: 4 2 -1 0 1 The graph has no negative edge cycle
Algorithm
bellmanFord(dist, pred, source)
Input − Distance list, the predecessor list, and the source vertex.
Output − True, when a negative cycle is found.
Begin iCount := 1 maxEdge := n * (n - 1) / 2 //n is number of vertices for all vertices v of the graph, do dist[v] := ∞ pred[v] := Ď• done dist[source] := 0 eCount := number of edges present in the graph create edge list named edgeList while iCount < n, do for i := 0 to eCount, do if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i) pred[edgeList[i].v] := edgeList[i].u done done iCount := iCount + 1 for all vertices i in the graph, do if dist[edgeList[i].v] > dist[edgeList[i].u] + (cost[u,v] for edge i), then return true done return false End
Example
#include<iostream>
#include<iomanip>
#define V 5
#define INF 999
using namespace std;
//Cost matrix of the graph (directed) vertex 5
int costMat[V][V] = {
{0, 6, INF, 7, INF},
{INF, 0, 5, 8, -4},
{INF, -2, 0, INF, INF},
{INF, INF, -3, 0, 9},
{2, INF, 7, INF, 0}
};
typedef struct {
int u, v, cost;
}edge;
int isDiagraph() {
//check the graph is directed graph or not
int i, j;
for(i = 0; i<V; i++) {
for(j = 0; j<V; j++) {
if(costMat[i][j] != costMat[j][i]) {
return 1; //graph is directed
}
}
}
return 0;//graph is undirected
}
int makeEdgeList(edge *eList) {
//create edgelist from the edges of graph
int count = -1;
if(isDiagraph()) {
for(int i = 0; i<V; i++) {
for(int j = 0; j<V; j++) {
if(costMat[i][j] != 0 && costMat[i][j] != INF) {
count++; //edge find when graph is directed
eList[count].u = i; eList[count].v = j;
eList[count].cost = costMat[i][j];
}
}
}
}else {
for(int i = 0; i<V; i++) {
for(int j = 0; j<i; j++) {
if(costMat[i][j] != INF) {
count++; //edge find when graph is undirected
eList[count].u = i; eList[count].v = j;
eList[count].cost = costMat[i][j];
}
}
}
}
return count+1;
}
int bellmanFord(int *dist, int *pred,int src) {
int icount = 1, ecount, max = V*(V-1)/2;
edge edgeList[max];
for(int i = 0; i<V; i++) {
dist[i] = INF; //initialize with infinity
pred[i] = -1; //no predecessor found.
}
dist[src] = 0;//for starting vertex, distance is 0
ecount = makeEdgeList(edgeList); //edgeList formation
while(icount < V) { //number of iteration is (Vertex - 1)
for(int i = 0; i<ecount; i++) {
if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) { //relax edge and set predecessor
dist[edgeList[i].v] = dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v];
pred[edgeList[i].v] = edgeList[i].u;
}
}
icount++;
}
//test for negative cycle
for(int i = 0; i<ecount; i++) {
if(dist[edgeList[i].v] > dist[edgeList[i].u] + costMat[edgeList[i].u][edgeList[i].v]) {
return 1; //indicates the graph has negative cycle
}
}
return 0; //no negative cycle
}
void display(int *dist, int *pred) {
cout << "Vert: ";
for(int i = 0; i<V; i++)
cout <<setw(3) << i << " ";
cout << endl;
cout << "Dist: ";
for(int i = 0; i<V; i++)
cout << setw(3) << dist[i] << " ";
cout << endl;
cout << "Pred: ";
for(int i = 0; i<V; i++)
cout << setw(3) << pred[i] << " ";
cout << endl;
}
int main() {
int dist[V], pred[V], source, report;
source = 2;
report = bellmanFord(dist, pred, source);
cout << "Source Vertex: " << source<<endl;
display(dist, pred);
if(report)
cout << "The graph has a negative edge cycle" << endl;
else
cout << "The graph has no negative edge cycle" << endl;
}Output
Source Vertex: 2 Vert: 0 1 2 3 4 Dist: -4 -2 0 3 -6 Pred: 4 2 -1 0 1 The graph has no negative edge cycle
Updated on: 16-Jun-2020
3K+ Views
Advertisements