Ford Fulkerson Algorithm

The Ford-Fulkerson algorithm is used to detect maximum flow from start vertex to sink vertex in a given graph. In this graph, every edge has the capacity. Two vertices are provided named Source and Sink. The source vertex has all outward edge, no inward edge, and the sink will have all inward edge no outward edge.

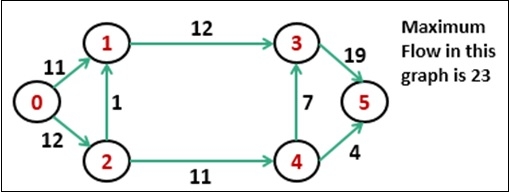
There are some constraints:

• Flow on an edge doesn’t exceed the given capacity of that graph.
• Incoming flow and outgoing flow will also equal for every edge, except the source and the sink.

Input and Output

Input:
The adjacency matrix:
0 10 0 10 0  0
0  0 4  2 8  0
0  0 0  0 0 10
0  0 0  0 9  0
0  0 6  0 0 10
0  0 0  0 0  0

Output:
Maximum flow is: 19

Algorithm

bfs(vert, start, sink)

Input: The vertices list, the start node, and the sink node.

Output − True when the sink is visited.

Begin
   initially mark all nodes as unvisited
   state of start as visited
   predecessor of start node is φ
   insert start into the queue qu
   while qu is not empty, do
      delete element from queue and set to vertex u
      for all vertices i, in the residual graph, do
         if u and i are connected, and i is unvisited, then
            add vertex i into the queue
            predecessor of i is u
            mark i as visited
      done
   done
   return true if state of sink vertex is visited
End

fordFulkerson(vert, source, sink)

Input: The vertices list, the source vertex, and the sink vertex.

Output − The maximum flow from start to sink.

Begin
   create a residual graph and copy given graph into it
   while bfs(vert, source, sink) is true, do
      pathFlow := ∞
      v := sink vertex
      while v ≠ start vertex, do
         u := predecessor of v
         pathFlow := minimum of pathFlow and residualGraph[u, v]
         v := predecessor of v
      done

      v := sink vertex
      while v ≠ start vertex, do
         u := predecessor of v
         residualGraph[u,v] := residualGraph[u,v] – pathFlow
         residualGraph[v,u] := residualGraph[v,u] – pathFlow
         v := predecessor of v
      done

      maFlow := maxFlow + pathFlow
   done
   return maxFlow
End

Example

#include<iostream>
#include<queue>
#define NODE 6
using namespace std;

typedef struct node {
   int val;
   int state; //status
   int pred; //predecessor
}node;

int minimum(int a, int b) {
   return (a<b)?a:b;
}

int resGraph[NODE][NODE];

/* int graph[NODE][NODE] = {
   {0, 16, 13, 0, 0, 0},
   {0, 0, 10, 12, 0, 0},
   {0, 4, 0, 0, 14, 0},
   {0, 0, 9, 0, 0, 20},
   {0, 0, 0, 7, 0, 4},
   {0, 0, 0, 0, 0, 0}
}; */

int graph[NODE][NODE] = {
   {0, 10, 0, 10, 0, 0},
   {0, 0, 4, 2, 8, 0},
   {0, 0, 0, 0, 0, 10},
   {0, 0, 0, 0, 9, 0},
   {0, 0, 6, 0, 0, 10},
   {0, 0, 0, 0, 0, 0}
};
                   
int bfs(node *vert, node start, node sink) {
   node u;
   int i, j;
   queue<node> que;

   for(i = 0; i<NODE; i++) {
      vert[i].state = 0;    //not visited
   }

   vert[start.val].state = 1;   //visited
   vert[start.val].pred = -1;   //no parent node
   que.push(start);   //insert starting node

   while(!que.empty()) {
      //delete from queue and print
      u = que.front();
      que.pop();

      for(i = 0; i<NODE; i++) {
         if(resGraph[u.val][i] > 0 && vert[i].state == 0) {
            que.push(vert[i]);
            vert[i].pred = u.val;
            vert[i].state = 1;
         }
      }
   }
   return (vert[sink.val].state == 1);
}

int fordFulkerson(node *vert, node source, node sink) {
   int maxFlow = 0;
   int u, v;

   for(int i = 0; i<NODE; i++) {
      for(int j = 0; j<NODE; j++) {
         resGraph[i][j] = graph[i][j];    //initially residual graph is main graph
      }
   }

   while(bfs(vert, source, sink)) {    //find augmented path using bfs algorithm
      int pathFlow = 999;//as infinity
      for(v = sink.val; v != source.val; v=vert[v].pred) {
         u = vert[v].pred;
         pathFlow = minimum(pathFlow, resGraph[u][v]);
      }

      for(v = sink.val; v != source.val; v=vert[v].pred) {
         u = vert[v].pred;
         resGraph[u][v] -= pathFlow;   //update residual capacity of edges
         resGraph[v][u] += pathFlow;   //update residual capacity of reverse edges
      }

      maxFlow += pathFlow;
   }
   return maxFlow;    //the overall max flow
}

int main() {
   node vertices[NODE];
   node source, sink;

   for(int i = 0; i<NODE; i++) {
      vertices[i].val = i;
   }

   source.val = 0;
   sink.val = 5;
   int maxFlow = fordFulkerson(vertices, source, sink);
   cout << "Maximum flow is: " << maxFlow << endl;
}

Output

Maximum flow is: 19