Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Apothem of a n-sided regular polygon in C++
n-sided regular polygon is a closed figure of n sides that has all sides and angles of equal length. The below figure shows a 6 sided regular polygon commonly known as hexagon.
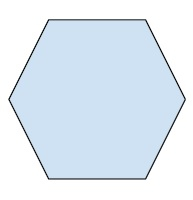
Apothem is a line in the polygon that connects the center of the figure to the side. And it is perpendicular to one of its sides that makes it smallest in length.
Now, let drive the formula for its length.
The angle made by the side of an n sided polygon is 360/n.
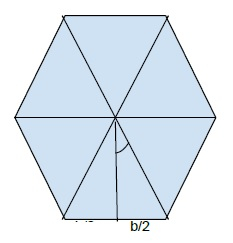
Now, as in the figure, the angle is equal to (360 / n )/2 = 180 /n
Now taking the triangle, we can conclude that
tan ø = b/2 / h = b/2h 2h * tan ø = b h = b/2*tanø , ø = 180 /n h = b/2*tan(180/n)
Let's implement this to a program to find the length of apothem when the number of sides and length of each side of the polygon are given.
Formula
Given n = number of side , b = length of each side. h = length of apothem, h = b/2 * tan(180/n)
Example
#include<iostream>
#include <math.h>
using namespace std;
void apothemLength(int n, float a){
if (a < 0 && n < 0)
cout<<"invalid values";
else
cout<<"the length of apothem = "<< (a/(2*tan((180/n)*3.14159/180)));
}
int main(){
float a = 12;
int n = 9;
apothemLength(n, a);
return 0;
}Output
the length of apothem = 16.4849
Updated on: 24-Oct-2019
160 Views
Advertisements