Area of a n-sided regular polygon with given side length in C++

A regular polygon with n sides is a two-dimensional shape with n equal-length sides and n equal interior angles. It is both equilateral and equiangular (all sides are equal and all angles are equal).

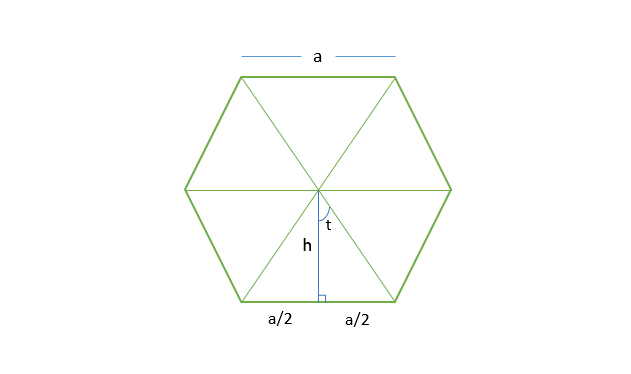
In the above diagram, we see that the polygon can be divided into n equal triangles. For one of the triangles, the complete angle at the center can be divided into = 2pi/n

• So, angle t = pi/n
• Now, tan(t) = a/2*h
• So, h = a/(2*tan(t))
• Area of each triangle = (base * height)/2 = a * a/(4*tan(t))

So, area of the polygon: (n*a^2)/(4*tan(t))

We are given a regular polygon with n sides, each of side length a. Our task is to find the area of the polygon using C++ program.

Let's see the following example scenarios to understand the problem better.

Scenario 1

Input: n = 6, a = 5
Output: Area = 64.952
Explanation: Substitute the given input in the above formula:
6*25/4*tan(pi/6)
150/4*0.577 = 150/2.309 = 64.95

Scenario 2

Input: n = 8, a = 7
Output: Area = 236.593
Explanation: Substitute the given input in the above formula:
8*49/4*tan(pi/8)
392/4*0.414 = 392/1.656 = 236.95

Calculating Area of N-Sided Regular Polygon in C++

To calculate the area of an n-sided regular polygon, we use the following formula:

Area = (n x a2) / (4 x tan(π / n))

Where:

• n is the number of sides,
• a is the length of each side,
• π / n is the central angle in radians.

To convert π to a numeric value, use π = 3.14159, so the angle becomes 3.14159 / n.

This formula is valid only for regular polygons, where all sides and angles are equal.

C++ Program to Compute Area of N-sided Polygon

The following example shows how you can calculate the area of a polygon when the coordinates of its n ordered vertices are given:

#include <iostream>
#include <cmath>
using namespace std;
int main() {
   // number of sides;
   float n = 6;
   // length of each side;
   float a = 5;
   // Convert degrees to radians
   float angle = 3.14159 / n;
   // Area of a regular polygon = (n * a^2) / (4 * tan(?/n))
   float area = (n * a * a) / (4 * tan(angle));
   cout<< "Area = "<<area << endl;
   return 0;
}

Following is the output:

Area = 64.952