Angle between two Planes in 3D in C Program?

In 3D geometry, planes are flat surfaces extending infinitely in space. When two planes intersect, they form a line, and the angle between them becomes an important geometric measure.

In this article, we will learn how to calculate the angle between two planes in 3D space using a C program.

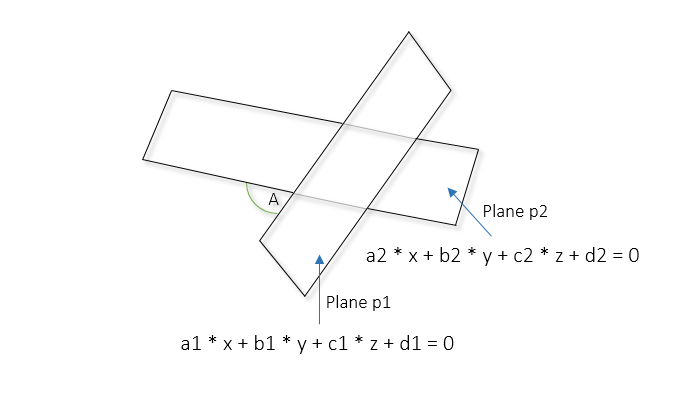
The diagram below illustrates two planes intersecting in 3D space. These planes can be represented by the following equations:

Equation

P1: a1 * x + b1 * y + c1 * z + d1 = 0  
P2: a2 * x + b2 * y + c2 * z + d2 = 0

Our task is to determine the angle between these two planes using their normal vectors in three-dimensional space.

Example Scenario

Let's go through this example scenario to understand the problem more clearly:

Input: a1 = 1, b1 = 1, c1 = 2, d1 = 1, a2 = 2, b2 = -1, c2 = 1, d2 = -4
Output: Angle A = 60.0 degree
Explanation:
Plane 1: P1: 1x + 1y + 2z + 1 = 0 ? Normal vector n? = (1, 1, 2)
Plane 2: P2: 2x - 1y + 1z - 4 = 0 ? Normal vector n? = (2, -1, 1)
So, the angle A => cos(A) = vec(n1).vec(n2)/mag(n1).mag(n2)
cos(A) = (1*2 + 1*-1 + 2*1) / (sqrt(1^2+1^2+2^2)*sqrt(2^2+(-1)^2+1^2))
cos(A) = (2 - 1 + 2) / sqrt(6)*sqrt(6)
cos(A) = 3/6 => cos(A) = ½ => A = cos'(1/2) => A = 60 Degree

Finding the Angle Between Two Planes in 3D Using C++

To find the angle between two planes in 3D space, we can use a direct mathematical approach (provided the equations of the planes are known).

Let the equations (as discussed above) of the two planes be:

P1: a1 * x + b1 * y + c1 * z + d1 = 0 
P2: a2 * x + b2 * y + c2 * z + d2 = 0 

Here, (a1, b1, c1) and (a2, b2, c2) are the direction ratios of the normal vectors to planes P1 and P2, respectively.

The angle between two planes is the same as the angle between their normal vectors. This angle can be calculated using the dot product formula:

cos(A) = (a1*a2+b1*b2+c1*c2) / sqrt(a1*a1+b1*b1+c1*c1)*sqrt(a2*a2+b2*b2+c2*c2)
Using inverse property, we get:
A = cos'((a1*a2+b1*b2+c1*c2) / sqrt(a1*a1+b1*b1+c1*c1)*sqrt(a2*a2+b2*b2+c2*c2))

C Program to Find Angle between two Planes in 3D

Following is the C++ program to find the angle between two planes in 3D:

#include <bits/stdc++.h> 
#include<math.h>
using namespace std;
void distance(float a1, float b1, float c1, float a2, float b2, float c2){
   float d = (a1 * a2 + b1 * b2 + c1 * c2);
   float e1 = sqrt(a1 * a1 + b1 * b1 + c1 * c1);
   float e2 = sqrt(a2 * a2 + b2 * b2 + c2 * c2);
   d = d / (e1 * e2);
   float pi = 3.14159;
   float A = (180 / pi) * (acos(d));
   cout << "Angle A = " << A << " degree";
}
int main()
{
   float a1 = 1;
   float b1 = 1;
   float c1 = 2;
   float d1 = 1;
   float a2 = 2;
   float b2 = -1;
   float c2 = 1;
   float d2 = -4;
   distance(a1, b1, c1, a2, b2, c2);
   return 0;
}

Following is the output:

Angle A = 60 degree