Angle between a chord and a tangent when angle in the alternate segment is given in C++?

In this problem, we are given a circle whose chord and tangent meet at a particular point. The angle in the alternate segment of a circle is given. We need to find the angle between the chord and the tangent.

According to the Alternate Segment Theorem the angle between a chord and a tangent is equal to the angle in the alternate segment of the circle.

Chord and Tangent

• The chord of a circle can be defined as the line segment joining any two points on a circle.

• A tangent is a straight line that touches a circle at only one point.

Scenario

Input: z = 40
Output: 40 degrees

Let's understand through the following diagram:

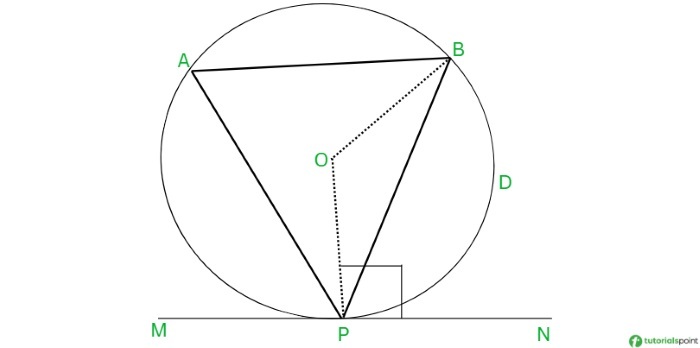
From the above diagram, we can see we have to prove angle BPN = angle PAB, i.e., the angle between the chord, tangent, and the alternate segment angle. Let's prove this:

• Draw the center of the circle at point O.

• Draw the radius OB and OP. Since we can say angle OPN is a right angle. (angle OPN = 90 degree)

• AS, OP is perpendicular to MN.(because OP is the radius and MN is a tangent, and P is the point where the radius and tangent meet.)

• So, angle OPN = 90 degrees. Also, OP = OB (radii).

• In triangle OPB, angle OPB is congruent with angle OBP = x degrees.(Property of an isosceles triangle).

• Arc PDB subtends angle POB at the center and subtends angle PAB at the circle. So, angle POB = 2 angle PAB and angle POB + X degree + x degree = 180 degree.

• By solving this, angle PAB = 90 degrees - x degrees (alternate segment).

• Now, solve this Angle OPN = angle OPB + angle BPN by putting values [ (OPN = 90, OPB = X)]

• By solving this, angle BPN = 90 degrees - x degrees (chord and tangent angle).

Hence, we can see equations 1 and 2 are equal, so it is proven that the angle between a chord and a tangent is equal to the angle in the alternate segment of the circle.

C++ Program 

Following is a C++ program to find the angle between a chord and a tangent when the angle in the alternate segment is given:

#include <iostream>
using namespace std;

int main() {
   // The alternate segment 
   double angleInAlternateSegment = 40;
   // According to the Alternate Segment Theorem:
   double angleBetweenChordAndTangent = angleInAlternateSegment;
   cout << "Angle in the alternate segment: " << angleInAlternateSegment << " degrees" << endl;
   cout << "Angle between the chord and the tangent: " << angleBetweenChordAndTangent << " degrees" << endl;

   return 0;
}

Following is the output of the above program:

Angle in the alternate segment: 40 degrees
Angle between the chord and the tangent: 40 degrees