Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Amplifier Gains – Functions, Problems & Solutions
Function of Amplifiers
Amplifiers boost up or amplify weak signals. Repeaters are good examples of amplifying devices. They are present in few to several numbers at intermediate points between the transmitter and receiver, depending on the actual distance between the two. Periodic amplification at intermediate stations between the transmitter and receiver ensures that there is a desired level of signal-to-noise ratio (SNR) maintained with the signal to successfully complete the final mile of transmission.
Understanding Amplifier Gains
Example 1
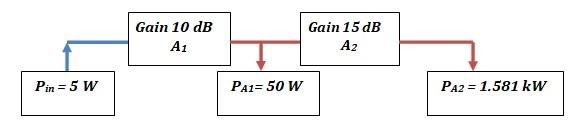
If in a two-amplifier system where the amplifiers are cascaded in series, the first amplifier provides a gain of 10 dB while the second amplifier provides a gain of 15 dB, what is the overall amplification of the signal at the output of the second amplifier with respect to the input signal at the first amplifier?
Approach
It is given that input signal power is 5 W. We know that multiplications on the linear scale become additions on the logarithmic scale. We also know that the overall gain of such a cascaded amplifier system is the product of gains of the individual amplifiers when considering their values to be in the linear scale. When we translate these linear scale values to a logarithmic scale, we can then add gains of the individual amplifiers to arrive at the overall gain of the amplifier system. It is easier to perform additions than multiplications and thus, the gains are expressed in dB so that the final gain can be computed by just adding the gains provided by the individual amplifiers.
$$Power\:gain(dB)=10log_{10}(\frac{P_{out}}{P_{ref}})=10log_{10}(\frac{P_{out}}{P_{in}})=10log_{10}(\frac{P_{A1}}{P_{in}})$$
$$10dB=10log_{10}(\frac{P_{A1}}{P_{in}})=10log_{10}(\frac{P_{A1}}{5W})$$
$$10log_{10}(\frac{P_{A1}}{5W})=\frac{10}{10}=1$$
$$(\frac{P_{A1}}{5W})=10^{1}=10\Rightarrow\:P_{A1}=(10)(5W)=50W$$
It can be observed that the signal power level at the output of the first amplifier is 50 W, which is 10 times higher than the power of the input signal. Thus, the amplification factor is 10 which also corresponds to a 10 dB increase in the input power level. Thus, we can say that an increase of 10 dB in power level corresponds to having ten times the power that was initially available.
10 dB increase in input power ⇒ Multiplying the input power by 10
Let us discuss the second stage of amplification. The power available at the output of the first amplifier is 50 W. We know that the second amplifier is designed to provide a gain of 15 dB. So, what will the final output power level be? We follow the same procedure. The only difference lies in replacing the value of initial input power or reference power by its new value which is calculated as 50 W.
$$15dB=10log_{10}(\frac{P_{A2}}{P_{A1}})=10log_{10}(\frac{P_{A2}}{50W})$$
$$log_{10}(\frac{P_{A2}}{50W})=\frac{15}{10}=1.5$$
$$(\frac{P_{A2}}{50W})=10^{1.5}\sim\:31.622\Rightarrow\:P_{A2}=(31.622)(50W)=1581.13W\sim\:1.581kW$$
We can observe that the power level available at the output of the first amplifier has been amplified by about 31.622 times thus giving us the final output power of 1.581 kW.
What is the overall amplification of this system? The answer is 316.22 which translates to 25 dB.
$$Overall\:gain=(10)(31.622)=316.22\equiv25dB=10dB+15dB$$
$$25dB=10log_{10}(\frac{P_{A2}}{P_{in}})$$
$$log_{10}(\frac{P_{A2}}{P_{in}})=2.5\Rightarrow\:(\frac{P_{A2}}{P_{in}})=10^{2.5}\sim\:316.22$$
Example 2
Let us consider an example that deals with voltage gain instead of power gain. Here voltage amplification is performed. Let us proceed with the same amplifier system and the same values of amplification.
One important fact to be known is that power is directly proportional to the square of the voltage.
$$P=\frac{V^{2}}{R}$$
$$P(dB)=\frac{V^{2}}{R}(dB)$$
$$10log_{10}P=10log_{10}(\frac{V^{2}}{R})$$
Considering unit resistance, we have
$$10log_{10}P=10log_{10}(V^{2})=20log_{10}V$$
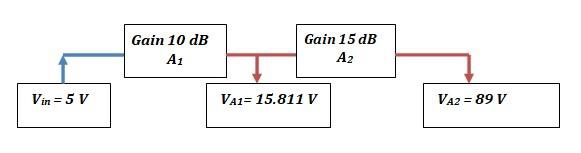
Let us find the values of VA1 and VA2.
$$Voltage\:gain(dB)=20log_{10}(\frac{V_{out}}{V_{ref}})=20log_{10}(\frac{V_{out}}{V_{in}})=20log_{10}(\frac{V_{A1}}{V_{in}})$$
$$10dB=20log_{10}(\frac{V_{A1}}{V_{in}})=20log_{10}(\frac{V_{A1}}{5V})$$
$$log_{10}(\frac{V_{A1}}{5V})=\frac{10}{20}=0.5$$
$$(\frac{V_{A1}}{5V})=10^{0.5}=3.162;\:V_{A1}=15.811V$$
10 dB increase in input voltage ⇒ Multiplying the input voltage by √10
Similarly,
20 dB increase in input voltage ⇒ Multiplying the input voltage by 10
We now calculate VA2. The input voltage is now 15.811 V.
$$15dB=20log_{10}(\frac{V_{A2}}{V_{A1}})=20log_{10}(\frac{V_{A2}}{15.811V})$$
$$log_{10}(\frac{V_{A2}}{15.811V})=\frac{15}{20}=0.75$$
$$(\frac{V_{A2}}{15.811V})=10^{0.75}=5.623;\:V_{A2}\sim\:89V$$
$$Overall\:gain=(3.162)(5.623)=17.8\equiv25dB=10dB+15dB$$
$$25dB=20log_{10}(\frac{P_{A2}}{P_{in}})$$
$$10log_{10}(\frac{P_{A2}}{P_{in}})=1.25\Rightarrow\:(\frac{P_{A2}}{P_{in}})=10^{1.25}\sim\:17.8$$
We can also note that increasing the power level by 3 dB is equivalent to doubling the initially available power.
QUICK TIP
If an amplifier provides power amplification by 3 dB, it means that the power available at the output of the amplifier is twice its initial value.
If an amplifier provides voltage amplification by 6 dB, it means that the voltage available at the amplifier output is twice its initial value.
387 Views
