Shortest path with exactly k Edges

One directed graph is provided with the weight between each pair of vertices, and two vertices u and v are also provided. Our task is to find the shortest distance from vertex u to vertex v, with exactly k number of edges. 

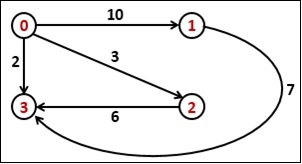
To solve this problem, we will start from vertex u and go to all adjacent vertices and recur for adjacent vertices using the k value as k - 1.

Input and Output

Input:
The cost matrix of the graph.
0 10 3 2
∞  0 ∞ 7
∞  ∞ 0 6
∞  ∞ ∞ 0

Output:
Weight of the shortest path is 9

Algorithm

shortKEdgePath(u, v, edge)

Input − Vertex u and v, and a number of edges.

Output − Distance of shortest path.

Begin
   if edge = 0 and u = v, then
      return 0
   if edge = 1 and cost[u, v] ≠ ∞, then
      return cost[u, v]
   if edge 
Example
#include 
#define NODE 4
#define INF INT_MAX
using namespace std;

int cost[NODE][NODE] = {
   {0, 10, 3, 2},
   {INF, 0, INF, 7},
   {INF, INF, 0, 6},
   {INF, INF, INF, 0}
};

int minimum(int a, int b) {
   return (a
Output
Weight of the shortest path is 9