Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
2-3 Trees - Data Structures and Algorithms in C++
A 2-3 Tree is a type of tree in data structures in which every node of the tree is either a 2 node
or 3 nodes. It is a special type of B-Tree with order 3.
A 2 node in the tree is one which has one data part and two child nodes.
A 3 node in the tree is one which has two data parts and three child nodes.
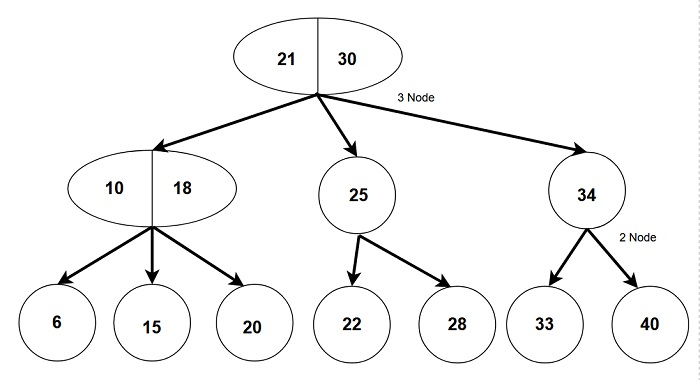
Fig:- A 2-3 tree
Properties of a 2-3 Tree:-
Every internal node is either a 2 node or a 3 node.
A node containing one data part can be a 2 node with exactly 2 children or a leaf node with no children.
A node containing two data parts can only be a 3 node with exactly 3 children.
All leaf nodes are always at the same level.
A 2-3 tree is always a height balanced tree.
Search operations are fast and efficient in a 2-3 tree.
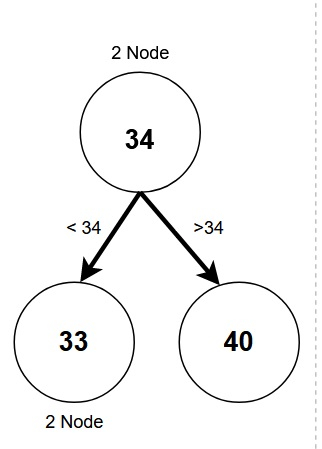
2 Node:-
Exactly two children.
Left child with smaller weight.
Right child with greater weight.
Can be a leaf node with no child.
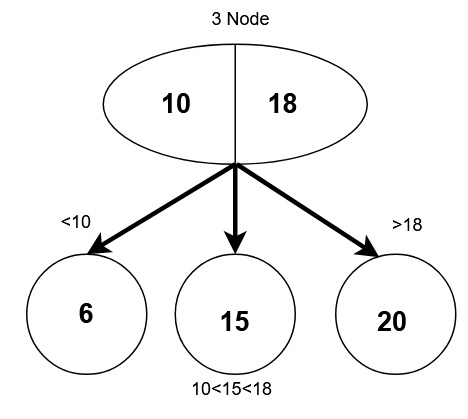
3 Node:-
Exactly three children.
2 data values.
Left child with weight smaller than left data value.
Middle child with weight in between both data values.
Right child with weight greater than right data value.
Can never be a leaf node.
Operations in a 2-3 Tree:-
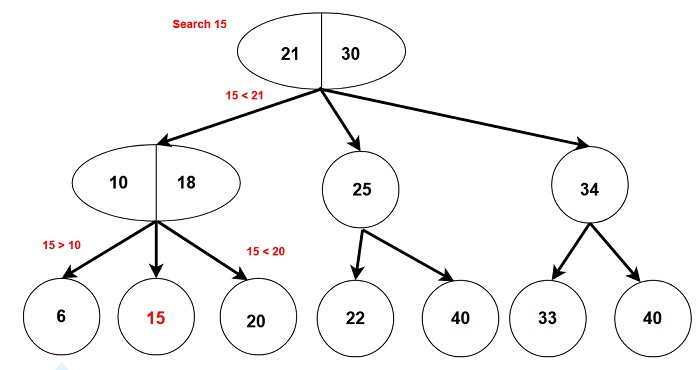
1. Searching in a 2-3 tree
Similar to the search operation in a binary search tree as the data is sorted.
To search X in a 2-3 tree.
If tree is empty → return False
If we reach root node then return False (not found)
If X is less than the left data part, then search the left subtree
If X is greater than left data and more than right data, search the middle subtree.
If X is greater than the right data part, then search right subtree.
2. Inserting a node in a 2-3 tree
To insert X in a 2-3 tree.
If the tree is empty → Add X as root.
Search for the right position of X and add it as a leaf node.
If there is a leaf node with one data part, add X with and leaf node becomes 2 - Node.
If the leaf node has two data parts, add X. Split temporary 3-nodes and move data to parent nodes according to the sorting order.
Make 2-3 tree and add nodes in order → 10, 5, 8, 15, 23, 21
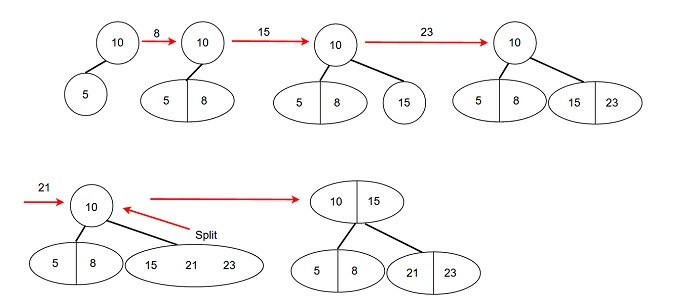
3. Deletion of a node in a 2-3 tree
To delete X in a 2-3 tree.
If the tree is empty return false.
Search for the position of X and delete it, then adjust the tree.
If X is part of 3 node delete X and adjust left value and middle value. Also adjust node’s ancestor’s left and middle value if necessary.
If X is part of 2 node then adjust and split the tree in a recursive manner arranging nodes in sorted order.
5K+ Views
