Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Optimal Binary Search Trees in Data Structures
A set of integers are given in the sorted order and another array freq to frequency count. Our task is to create a binary search tree with those data to find minimum cost for all searches.
An auxiliary array cost[n, n] is created to solve and store the solution of sub problems. Cost matrix will hold the data to solve the problem in bottom up manner.
Input − The key values as node and the frequency.
Keys = {10, 12, 20}
Frequency = {34, 8, 50}Output − The minimum cost is 142.
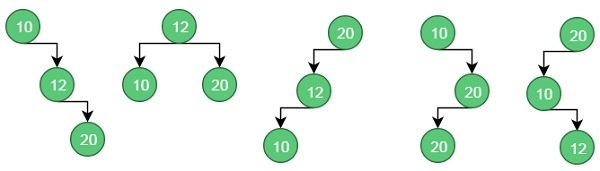
These are possible BST from the given values.
For case 1, the cost is: (34*1) + (8*2) + (50*3) = 200
For case 2, the cost is: (8*1) + (34*2) + (50*2) = 176.
Similarly, for case 5, the cost is: (50*1) + (34 * 2) + (8 * 3) = 142 (Minimum)
Algorithm
optCostBst(keys, freq, n) Input: Keys to insert in BST, frequency for each keys, number of keys. Output: Minimum cost to make optimal BST. Begin define cost matrix of size n x n for i in range 0 to n-1, do cost[i, i] := freq[i] done for length in range 2 to n, do for i in range 0 to (n-length+1), do j := i + length – 1 cost[i, j] := ∞ for r in range i to j, done if r > i, then c := cost[i, r-1] else c := 0 if r < j, then c := c + cost[r+1, j] c := c + sum of frequency from i to j if c < cost[i, j], then cost[i, j] := c done done done return cost[0, n-1] End
Example
#include <iostream>
using namespace std;
int sum(int freq[], int low, int high){ //sum of frequency from low to high range
int sum = 0;
for (int k = low; k <=high; k++)
sum += freq[k];
return sum;
}
int minCostBST(int keys[], int freq[], int n){
int cost[n][n];
for (int i = 0; i < n; i++) //when only one key, move along diagonal elements
cost[i][i] = freq[i];
for (int length=2; length<=n; length++){
for (int i=0; i<=n-length+1; i++){ //from 0th row to n-length+1 row as i
int j = i+length-1;
cost[i][j] = INT_MAX; //initially store to infinity
for (int r=i; r<=j; r++){
//find cost when r is root of subtree
int c = ((r > i)?cost[i][r-1]:0)+((r < j)?cost[r+1][j]:0)+sum(freq, i, j);
if (c < cost[i][j])
cost[i][j] = c;
}
}
}
return cost[0][n-1];
}
int main(){
int keys[] = {10, 12, 20};
int freq[] = {34, 8, 50};
int n = 3;
cout << "Cost of Optimal BST is: "<< minCostBST(keys, freq, n);
}Output
Cost of Optimal BST is: 142
Updated on: 27-Aug-2019
962 Views
Advertisements